大家好,我是科学羊,这里是数学专栏第3季第11篇。
今天我们来谈谈矩阵!
在高等数学的宏大世界里,微积分和线性代数犹如基础的砖石,铺就了理解复杂数学概念的道路。
对于广大非理工科的学子而言,这两门课程往往是大学数学学习的全部,这也是考研数学的必须课程!
微积分不仅是一门课程,它更是一种锻炼逻辑思维的方式,而线性代数的应用范围如此广泛,以至于工作和日常生活中处处可见其身影。
我们此前已经涉足了线性代数的领域,虽然并未明言。实际上,我们讨论的向量代数正是线性代数中最基础也是最为关键的组成部分。
矩阵,作为线性代数中使用频率最高的概念,其实质和用途引人入胜。
什么是矩阵?
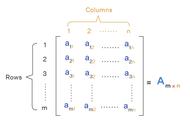
矩阵是一个按照行和列排列的矩形阵列,其中的每一个元素都可以通过其行号和列号唯一确定。数学上,一个m*n的矩阵表示为:

简单来说,矩阵就是数字的有序排列,通过行和列的方式进行组织,每行和每列的数字数量保持一致。
比如一个3x4的矩阵,意味着它拥有3行4列。

矩阵之所以存在,并非无缘无故,而是向量概念的自然扩展。
也就是将多个向量放在一起,显然最直观的方式,就是把它们一行行排起来,这形成了一个有M行N列的矩阵。这就是矩阵的由来。
以招聘为例,一个公司将各种考核指标综合为N个维度,每个岗位的能力要求便形成了一个N维向量。随着不同部门、不同岗位的向量汇聚,最直观的表示方法便是将这些向量按行排列,形成一个M行N列的矩阵,揭示了矩阵的由来。
矩阵的历史比较晚近,直到1850年才由英国数学家西尔维斯特(James Joseph Sylvester)正式命名。
尽管有观点认为早在古代中国、日本、意大利和阿拉伯等地就有矩阵的原型,但这些与今天我们所用的数学矩阵概念相去甚远。
真正的矩阵概念包含了特定的含义赋予以及一套完备的计算方法,这使得矩阵成为了解决问题的强大工具。
矩阵的加法和乘法是其两种基本运算。
通过矩阵加法,我们可以将一般性要求与针对特定情境的调整结合起来,体现在具体国家的员工要求上。
比如有个矩阵:

那么,当我们进行A B时,只要把两个矩阵中相应位置的元素逐一相加即可,也就是说矩阵A加矩阵B,会得到下面的结果

而矩阵乘法的应用更为广泛,尤其在金融领域,它能够帮助投资者根据不同的投资偏好和风险承受能力计算潜在的回报。(这部分我们明天重点下一节在机器人中再讲)
我们将向量和矩阵的乘法作为例子,展示了如何通过这种运算方式处理实际问题,例如确定投资的最优选择。这种运算不仅仅是简单的算术操作,而是一种批量处理问题的方法,特别适合处理高维度数据。
矩阵运算的引入,不仅仅是数学领域的一大进步,它更是一种全新的思考方式,将单个计算转变为大批量处理,这一思维方式对今天信息时代至关重要。
最后,我们探讨了线性代数之所以称之为“线性”的原因,即其运算和表达都与线性方程组紧密相关,揭示了直线、平面及其它线性形态的本质。
虽然自然界中的许多问题并非严格的线性,但将其近似为线性问题,可以让我们利用线性代数的工具来寻求解决方案。
通过这一系列的探讨,我们不仅加深了对微积分和线性代数的理解,也为即将介绍的微积分主题打下了坚实的基础,展现了数学之美,以及它在现实世界中无限的应用潜力。
那么矩阵到底有什么用?
矩阵,这一简洁而强大的数学工具,广泛应用于各个领域,从纯数学研究到实际的工程问题解决,都离不开矩阵的支持。
其用途可以概括为以下几个方面:
1. 线性方程组的求解
矩阵是解决线性方程组问题的一种有效工具。通过将线性方程组表示为矩阵形式,可以使用矩阵运算(如矩阵求逆或行列式计算)来找到方程组的解。
这在数学、物理学及工程学等领域的问题求解中至关重要。
2. 线性变换与图形处理
在计算机图形学中,矩阵被用来表示和执行图形的线性变换,包括旋转、缩放、平移等操作。
通过对矩阵进行运算,可以高效地对图像进行变换,这在视频游戏开发、动画制作、CAD(计算机辅助设计)等领域中有着广泛应用。
3. 经济学中的输入输出分析
如前所述,矩阵在经济学中的输入输出分析中扮演着重要角色。通过构建经济活动的矩阵模型,经济学家可以分析各个产业之间的相互依赖关系,预测经济政策变化对产业的影响。
4. 量子力学与统计学
在量子力学中,矩阵用于描述物理系统的状态和演化。矩阵力学是量子力学的一个基本框架。
同时,在统计学中,矩阵运算用于处理和分析大量数据,如协方差矩阵分析、主成分分析(PCA)等,对于数据降维、特征提取等任务至关重要。
5. 机器学习与数据科学
在机器学习和数据科学领域,矩阵用于表示和处理数据集,支持如线性回归、逻辑回归、神经网络等算法的实现。矩阵运算优化了这些算法的计算过程,使得处理大规模数据集成为可能。
6. 控制理论
在自动控制领域,矩阵用于设计和分析控制系统。系统的动态行为可以用状态空间模型来描述,该模型本质上是一组线性微分方程,可以通过矩阵形式表示和求解。
矩阵的应用遍及科学研究、工程技术、经济管理等各个领域,它不仅是一种处理数学问题的强大工具,也是连接理论与实践、简化和优化解决方案的桥梁。
通过矩阵,我们能更加深入地理解复杂系统的本质,更加高效地处理和分析大规模数据。
最后,

不得不说,矩阵有用最多的就是我们行业了,因为我所处的机器人行业,机器人运动学就是建立在矩阵的基础上。
很多人问我,矩阵在机器人学到底有什么用,实际矩阵之所以有用,是因为它可以直观去表示机器人所处笛卡尔坐标系下位置和姿态(角度)。
我们知道机械手负责搬运就是需要知道被搬运物体的空间位置和角度,所以翻译在机器人这里就表示机器人的位置矩阵和姿态旋转矩阵。所以矩阵在工程行业是一个很重要的数学基础!
同样,游戏开发也会用到矩阵,一个角色的姿态和位置,也是通过矩阵去表示。
这部分我们下一节详谈!
好,今天就先这样啦!