想象一下,你走进了一个充满神秘数字的室内花园。在这个花园里,每一朵花都由数字组成,每一片叶子都是一个数字序列。这个花园的每一部分都是用精心排列的数字阵列构建的。这个场景,虽然听起来像是科幻小说的一部分,其实是一个比喻,用来描绘一个数学上的概念——矩阵。
矩阵,这个可能听起来有些陌生的词汇,实际上是我们日常生活中无处不在的一部分。从社交媒体上的好友网络,到电影中的特效制作,从精密的工程计算到简单的购物清单,矩阵无时无刻不在我们的生活中扮演着重要角色。它们是数学的一种强大工具,帮助我们组织和处理信息,解决复杂的问题。
但是,矩阵到底是什么呢?它们是怎么工作的?为什么矩阵在如此多的领域中都如此重要?本文将带你走进矩阵的世界,用通俗易懂的语言和生动的比喻,解开矩阵这个数学概念的神秘面纱。
接下来,我们将一起探索矩阵的基本概念、它们在数学中的作用,以及矩阵运算的特殊性。通过这些内容,你将会发现,矩阵不仅仅是干燥的数学符号,而是一个充满想象力和创造力的有趣世界。
让我们开始这趟旅程吧!

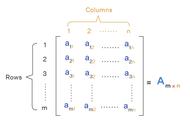
想要理解矩阵,我们首先得知道它长什么样子。试想你正在玩一个益智游戏,游戏中有一块块的小方格,每个方格里都填着一个数字。矩阵,就像是这样一个由数字填充的方格阵列。但与普通的游戏板不同,矩阵的每一个数字都有其独特的位置和意义,它们被整齐地排列在行和列中。就像一支精密排列的舞蹈队伍,每个舞者(数字)都在特定的位置上执行特定的动作。
在矩阵中,我们用行(水平排列的数字序列)和列(垂直排列的数字序列)来描述这个数字的舞蹈。例如,一个有三行两列的矩阵可能看起来像一个小型的电子表格,其中包含六个数字,每行两个。
矩阵并不是只存在于数学教科书中。它们实际上是我们日常生活中不可或缺的一部分。想象一下,你正在计划一次家庭度假。你可能会在纸上画出一个表格,列出每个目的地的旅行日期、预算和活动安排。这个表格,实际上就是一个矩阵的实例。它帮助你组织信息,使复杂的计划变得清晰易懂。
在更为复杂的应用中,例如在社交网络分析中,矩阵被用来表示人与人之间的关系。在这里,每个人被视为一个点,而他们之间的关系则通过矩阵中的数字来表示。矩阵可以告诉我们谁与谁是朋友,谁关注了谁,以及社交网络的整体结构。
通过这些例子,我们可以看到,矩阵不仅仅是抽象的数学概念,它们其实是一种强大的工具,帮助我们解决现实世界中的问题,从简单的日常任务到复杂的社会网络分析。

让我们将视角转向数学,探索矩阵在这个领域的作用。假设你是一名侦探,正在解决一个复杂的案件。案件涉及许多线索和嫌疑人,每个线索都可能指向不同的结论。在这个情景中,矩阵就像是一个线索组合器,它能帮助你整合和分析所有的信息,找出解决案件的方法。
在数学中,特别是在解决线性方程组时,矩阵扮演着类似的角色。线性方程组是由多个方程构成的集合,其中每个方程都像是一个线索,指向未知数的可能值。通过将这些方程表示为矩阵的形式,我们可以更加高效和清晰地处理它们。矩阵使我们能够用一种紧凑和系统的方式来表示和解决这些方程组,就像侦探使用线索板一样。
再进一步,矩阵在数学中的另一个重要应用是线性变换。想象你是一名魔术师,你的魔法棒可以使物体旋转、缩放或变形。在数学的世界里,矩阵就像是这样一根魔法棒。当应用于向量(一种数学对象,可以表示空间中的点或方向),矩阵可以使这些向量旋转、缩放或者以其他方式变换。
例如,在计算机图形学中,矩阵被用来操纵和变换图形。通过应用不同的矩阵,我们可以使图像旋转、缩放或扭曲,正如在电影或视频游戏中看到的那样。这种变换的能力使矩阵成为了设计和动画创作中不可或缺的工具。
通过这些例子,我们可以看到矩阵在数学中是如何使复杂问题变得简单,以及它们是如何作为变换的强大工具来使用。矩阵不仅帮助我们解决方程组,还让我们能够以创造性的方式操纵和变换对象。

矩阵的运算与我们在小学学到的基本数学运算有所不同。想象一下,如果日常的加减乘除就像是在一条直线上行走,那么矩阵的运算就像是在一个多层次的迷宫中探险。在这个迷宫里,每一步都不仅仅是简单的前进或后退,而是可能涉及多个维度的移动。
当我们将两个矩阵相加或相减时,这就像是在合并或区分两个不同的信息阵列。而矩阵乘法则更加复杂,它不是单纯的元素之间的相乘,而是行与列之间的一种交叉运算。这种乘法可以看作是一种信息转换过程,它将一个矩阵中的数据重新组合,生成一个全新的矩阵。
矩阵乘法的独特之处在于它反映了线性变换的组合。让我们用一个简单的比喻来理解这一点:假设你是一名导演,正在指导一部电影。在这个过程中,你需要先拍摄原始镜头(一个矩阵),然后对这些镜头进行编辑和特效处理(另一个矩阵)。矩阵乘法就像是这两个过程的结合:它将原始镜头和编辑效果合并,创造出最终的电影画面。
这种乘法的方式确保了变换的连贯性和系统性。它允许我们以一种结构化的方式来组合不同的操作,无论是在电影制作、物理模拟,还是在更抽象的数学分析中。通过矩阵乘法,我们能够将复杂的问题分解成更易于管理和理解的小部分。
总之,矩阵运算的特殊性在于它们提供了一种处理和组合高维数据的有效方式。这些运算不仅在数学上具有深刻的意义,而且在实际应用中也极为重要和有用。

矩阵不仅在理论数学中有着重要的地位,它们在现实世界的各个领域中也扮演着关键角色。让我们来看看矩阵是如何在科学、工程和计算机科学中发挥作用的。
在科学和工程领域,矩阵被用于解决各种各样的问题。比如说,一个工程师正在设计一座桥梁。他们会使用矩阵来计算和分析结构的力学性能,如承载能力和稳定性。矩阵帮助他们理解不同部分之间的相互作用,确保设计既安全又高效。
同样,在物理学中,矩阵被用来描述复杂的物理系统和现象,如量子力学中的状态和粒子的行为。在化学中,矩阵有助于研究分子的结构和反应过程。在生物学中,矩阵可以用来分析基因和蛋白质的网络。
在计算机科学和图形学领域,矩阵的应用更是无处不在。想象一下你正在玩一个视频游戏,游戏中的每一个角色、每一座建筑,甚至光线和阴影,都是通过矩阵变换来创建和操纵的。在这个虚拟世界里,矩阵使得开发者能够精确控制物体的移动、缩放和旋转,创造出逼真的三维效果。
此外,矩阵在计算机科学的其他领域,如数据分析、机器学习和人工智能中也发挥着重要作用。它们用于构建和训练模型,处理和分析大量数据,帮助我们从复杂的数据中提取有用的信息和洞见。
通过这些实际应用的例子,我们可以看到,矩阵不仅是数学的抽象概念,它们在帮助我们理解和改变世界方面起着至关重要的作用。矩阵的广泛应用说明了它们作为一种工具的强大和灵活性,无论是在解决具体的工程问题,还是在创造令人惊叹的数字艺术作品中。

当我们站在矩阵的巨大迷宫前,可以看到这个迷宫不仅是数学家的乐园,也是工程师、科学家、艺术家和计算机专家的实验场。矩阵的力量在于它的多功能性和普遍性,它能够将复杂的问题简化,使我们能够以新的视角来理解世界。
矩阵,这个起初可能看起来晦涩难懂的概念,实际上是我们日常生活中一个不可或缺的部分。它们帮助我们解决实际问题,推动科技发展,甚至创造艺术。无论是在设计一座桥梁、分析社交网络、制作电影特效,还是在更广泛的科学研究中,矩阵都扮演着关键的角色。
通过本文的探索,我们希望你能对矩阵有了更深入的理解和欣赏。矩阵不仅是数学的一部分,它们是我们理解复杂世界的一个强大工具。我们鼓励你继续探索和学习,发现矩阵在你的生活和工作中的更多应用。记住,每当你遇到一个数据阵列,不管是在纸上还是在电脑屏幕上,你都可能正在与矩阵打交道。
最后,我们邀请你加入这个充满奇迹的数学世界,去发现矩阵在你周围的无限可能性。这是一个既充满挑战又充满机遇的世界,等待着你去探索和创造。
欢迎关注我的*Renda_Zhang