注:其中第三个性质,可以把所有的X Y的各种情况展开,最后得出的结果就是这样的。
二:随机变量函数(复合随机)的数学期望1.理解

注:其实就是复合随机变量的期望,对于离散型,其主要是每个值增加了多少倍/减少了多少倍,但是概率不变,所以公式见上面;对于连续性随机变量,其实是一样的,每个点的概率没有变,所以就是变量本身的值发货所能了改变。
三:方差引入的意义:

求每次相对于均值的波动:

求波动的平方和:

注:其中第三个性质,可以把所有的X Y的各种情况展开,最后得出的结果就是这样的。
二:随机变量函数(复合随机)的数学期望1.理解

注:其实就是复合随机变量的期望,对于离散型,其主要是每个值增加了多少倍/减少了多少倍,但是概率不变,所以公式见上面;对于连续性随机变量,其实是一样的,每个点的概率没有变,所以就是变量本身的值发货所能了改变。
三:方差引入的意义:

求每次相对于均值的波动:

求波动的平方和:


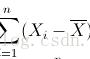



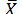










Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.