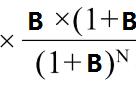等额本息法是指在还款期限内,每期还款金额相等的一种还款方式。推导等额本息法的公式如下:
设贷款总额为P,贷款期

限为n个月,年利率为r(以小数表示),每月还款额为A。
根据等额本息法,每月还款额A可以通过以下公式计算:
A = P * r * (1 r)^n / ((1 r)^n - 1)
其中,(1 r)^n表示(1 r)的n次方。
这个公式可以通过数学推导得到,具体推导过程如下:
设每月还款额为A,第一个月还款后,剩余贷款金额为P1 = P - A。
第二个月还款后,剩余贷款金额为P2 = P1 * (1 r) - A。
第三个月还款后,剩余贷款金额为P3 = P2 * (1 r) - A。
以此类推,第n个月还款后,剩余贷款金额为Pn = Pn-1 * (1 r) - A。
根据等额本息法,最后一期还款后,剩余贷款金额应为0,即Pn = 0。代入上述公式,得到:
0 = Pn-1 * (1 r) - A
将Pn-1代入上式,得到:
0 = (Pn-2 * (1 r) - A) * (1 r) - A
以此类推,将Pn-2、Pn-3等代入上式,最终得到:
0 = P * (1 r)^n - A * ((1 r)^n - 1)
整理上式,即可得到等额本息法的公式:
A = P * r * (1 r)^n / ((1 r)^n - 1)