模拟退火算法
simulated annealing algorithm
定义:一种根据固体退火原理、基于蒙特卡罗迭代求解策略的随机寻优算法。模拟高温金属的退火过程,通过扩大搜索范围以获取较优的解来改善局部搜索算法无法跳出局部最优的状况。局部搜索算法的推广,广泛应用于组合优化问题中。
学科:计算机科学技术_理论计算机科学_算法设计与分析
相关名词:组合优化 退火 局部最优 全局最优

图片来源:视觉中国
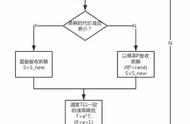
1983年柯克帕特里克等人在研究组合优化问题时,成功地将退火思想应用于求解问题,提出了“模拟退火算法”的概念。该算法是一种基于概率的优化算法,其灵感来源于固体退火过程的物理现象,即将固体加热到足够高的温度,然后使其慢慢冷却。加热时,随着温度升高,固体内部的粒子开始由有序变为无序,从而内能开始增大、分子或原子变得不稳定;降温时,固体粒子又逐渐恢复到有序状态,内能减少,从而分子或原子趋于稳定,而固体在每个温度下都能达到平衡态(即模拟退火算法中局部最优),在温度恢复到常温时,固体最终达到基态(即模拟退火算法中全局最优)。
在解决组合优化问题时,模拟退火算法具有计算过程简单、效率高以及能找到问题的近似解等优势。这得益于米特罗波利斯准则的特点,在高温状态下允许以一定概率接受较差的解,从而在一定程度上避免算法陷入局部最优的状态。该算法已在理论上被证明具有全局优化性能,因此,在工程中得到了广泛应用,如超大规模集成电路、生产调度、控制工程、机器学习、神经网络、信号处理等领域。其中,利用模拟退火算法进行VLSI的最优设计,如全局布线、布板、布局和逻辑最小化等,是目前模拟退火算法最成功的应用实例之一。
大量的模拟实验表明,模拟退火算法在求解组合优化问题时能产生令人满意的近似最优解,而且所用的时间也不是很长。但是,该算法也有一定的局限,其参数的可控性相对较差,往往需要反复迭代,才能获得最优解。