模拟退火算法(Simulated Annealing,SA)起源于固体物理学中的退火原理。固体物理学中的退火是指将固体加热至高温状态,然后缓慢冷却,使其内部结构逐渐趋于稳定。这个过程中,固体内部的原子会在不同温度下漫步运动,从而使得固体内部的结构逐渐趋于最优状态。
模拟退火算法最早由Kirkpatrick、Gelatt和Vecchi于1983年提出,是一种基于概率的全局优化算法。它通过模拟固体退火过程中的原子运动来寻找问题的全局最优解。模拟退火算法的基本思想是:在搜索过程中,允许一定概率接受劣解,以避免陷入局部最优解。
随着计算机技术的不断发展,模拟退火算法得到了广泛的应用。它被用于解决各种优化问题,如旅行商问题、图着色问题、装箱问题等。在实际应用中,模拟退火算法具有较好的鲁棒性和全局搜索能力,能够快速找到问题的最优解。
以下是一个简单的模拟退火算法实现的 Python 代码示例:
import math
import random
# 定义目标函数
def objective_function(x, y):
return math.sin(x) * math.cos(y) math.sin(2 * x y)
# 定义初始温度和终止温度
initial_temperature = 1000
final_temperature = 1
# 定义温度下降率
cooling_rate = 0.95
# 定义当前温度
current_temperature = initial_temperature
# 定义初始解
current_solution = (random.uniform(-10, 10), random.uniform(-10, 10))
# 迭代直到温度降到终止温度
while current_temperature > final_temperature:
# 在当前解的邻域中随机选择一个新解
new_solution = (current_solution[0] random.uniform(-1, 1), current_solution[1] random.uniform(-1, 1))
# 计算目标函数值的差
delta = objective_function(new_solution[0], new_solution[1]) - objective_function(current_solution[0], current_solution[1])
# 如果新解更优,则接受新解
if delta < 0:
current_solution = new_solution
# 否则以一定概率接受新解
else:
probability = math.exp(-delta / current_temperature)
if random.random() < probability:
current_solution = new_solution
# 降低温度
current_temperature *= cooling_rate
# 输出最终解和最优值
print("Final solution:", current_solution)
print("Final objective value:", objective_function(current_solution[0], current_solution[1]))
该代码实现了一个简单的模拟退火算法来求解一个二元函数的最优解。算法首先定义了目标函数、初始温度、终止温度和温度下降率等参数。然后从一个随机解开始迭代,每次随机选择一个新解,计算目标函数值的差,并根据一定的概率接受新解。最终输出最优解和最优值。
模拟退火算法基本思想是通过模拟物质的退火过程,寻找最优解或近似最优解。其核心思想是从一个初始解开始,通过一定的随机扰动,接受优化目标函数变差的解的概率逐渐减小,从而逐步趋向于全局最优解。
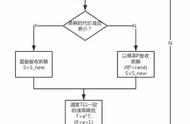
模拟退火算法的流程包括以下步骤:
1. 初始化:设定初始温度T0和初始解x0。
2. 产生新解:通过随机扰动当前解x,产生一个新解x'。
3. 计算能量差:计算新解x'与当前解x的能量差ΔE。
4. 判断是否接受新解:根据一定的概率接受新解,避免陷入局部最优解。
5. 降温:通过逐步降低温度T,减小接受劣解的概率,逐步趋向于全局最优解。
6. 终止条件:当温度降低到一定程度或达到一定迭代次数时,停止搜索,返回最优解。
基于模拟退火算法的超大规模集成电路研究主要是针对集成电路布线问题,通过优化电路布线的路径,提高电路的性能和可靠性。
优化目标主要是最小化电路延迟、最小化电路面积、最小化电路功耗等。
基于模拟退火算法的图像处理主要包括图像复原、图像去噪、图像分割等。其中,图像复原是指通过去除图像中的噪声和失真,恢复原始图像的过程;图像去噪是指通过去除图像中的噪声,提高图像质量;图像分割是指将图像分成不同的区域,用于图像分析和识别。
基于模拟退火算法的组合优化主要包括0-1背包问题、图着色问题、旅行商问题等。其中,0-1背包问题是指在给定的一组物品中,选择一些物品放入背包中,使得在不超过背包容量的前提下,背包中物品的总价值最大;图着色问题是指在给定的一张图中,用最少的颜色对所有节点进行染色,使得相邻节点颜色不同;旅行商问题是指在给定的多个城市之间,寻找一条最短的路径,使得每个城市恰好被访问一次。
背包问题是一类组合优化问题,给定一个背包和一些物品,每个物品有自己的重量和价值,要求在不超过背包容量的情况下,选择一些物品放入背包,使得背包中物品的总价值最大。
贪心算法是一种基于贪心策略的算法,它在每一步选择中都采取当前状态下最优的选择,以期望最终得到全局最优解。对于背包问题,贪心算法的贪心策略可以有多种选择,比如按照单位重量价值最大的顺序选择物品,或者按照重量从小到大的顺序选择物品。
具体来说,贪心算法的流程如下:
1. 计算每个物品的单位重量价值。
2. 按照单位重量价值从大到小的顺序排序。
3. 依次选择单位重量价值最大的物品,直到背包装满或没有物品可选为止。
贪心算法的优点是简单快速,适用于一些特殊情况下的优化问题。但是,贪心算法并不能保证得到全局最优解,因为它只考虑了当前状态下的最优选择,而没有考虑后续选择对最终结果的影响。对于背包问题,贪心算法可能会得到次优解或者不可行解。因此,在实际应用中,需要根据具体情况选择合适的算法来解决背包问题。
以下是一个背包问题的贪心算法实现,使用Python语言:
def knapsack_greedy(capacity, weights, values):
n = len(weights)
# 计算每个物品的单位重量价值
unit_values = [values[i] / weights[i] for i in range(n)]
# 按照单位重量价值从大到小排序
sorted_items = sorted(zip(weights, values, unit_values), key=lambda x: x[2], reverse=True)
total_value = 0
for weight, value, unit_value in sorted_items:
if capacity >= weight:
# 背包容量充足,可以放入当前物品
total_value = value
capacity -= weight
else:
# 背包容量不足,只能放入部分当前物品
total_value = unit_value * capacity
break
return total_value
函数knapsack_greedy的输入参数包括背包容量capacity、每个物品的重量weights和价值values。在函数中,首先计算每个物品的单位重量价值,并按照单位重量价值从大到小排序。然后,依次选择单位重量价值最大的物品,如果背包容量充足,则将该物品放入背包中,并将总价值增加该物品的价值;否则,只能放入部分该物品,并将总价值增加背包剩余容量所能容纳的价值。最后,返回总价值。
需要注意的是,贪心算法并不一定能够得到全局最优解,但是在某些情况下,贪心算法可以得到近似最优解,同时具有较高的效率。
局部最优解概念:
局部最优解指的是在某个局部范围内的最优解,它可能不是全局最优解。在贪心算法中,每一步的选择都是基于当前状态下的最优选择,因此得到的解可能只是局部最优解,而不是全局最优解。
贪心算法流程:
贪心算法的流程如下:
1. 定义问题的目标函数。
2. 按照一定规则将问题分解为若干个子问题。
3. 对每个子问题求解,得到子问题的最优解。
4. 将子问题的最优解合并得到原问题的解。
基于贪心算法的组合优化:
组合优化问题是指在离散的、有限的集合中,寻找最优的组合方案,使得目标函数达到最大或最小。基于贪心算法的组合优化是指在每一步选择中都采取当前状态下最优的选择,以期望最终得到全局最优解。
基于贪心算法的背包问题:
背包问题是一类组合优化问题,给定一个背包和一些物品,每个物品有自己的重量和价值,要求在不超过背包容量的情况下,选择一些物品放入背包,使得背包中物品的总价值最大。基于贪心算法的背包问题,每次选择单位重量价值最大的物品放入背包,直到背包装满或没有物品可选为止。
基于贪心算法的旅行商问题:
旅行商问题是指在给定的一些城市之间,求解一条经过每个城市一次且仅一次的最短路径,使得旅行商从起点出发,经过所有城市后回到起点。基于贪心算法的旅行商问题,每次选择距离当前城市最近的未访问过的城市作为下一个访问城市,直到所有城市都被访问过为止。虽然该算法不能保证得到全局最优解,但是在实际应用中,它可以得到较好的近似解。
,