2018
06
21
模拟退火算法
模拟退火算法 ( simulated anneal , SA) 求解最优化问题常用的算法,今天应用 SA 解决一元多次函数最小值的例子解释 SA 算法。

1 算法思想
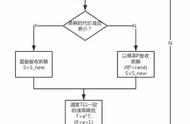
- 初始化:初始温度T,初始解状态S,是算法迭代的起点;
- 产生新解S′
- 计算增量ΔT = C(S′,S),其中C为评价函数:
- 若ΔT < 0,则接受 S′ 作为新的当前解,
- 否则以概率 exp(-ΔT/kT) 接受 S′ 作为新的当前解
- 如果满足终止条件则输出当前解作为最优解,结束程序,终止条件通常取为连续若干个新解都没有被接受时终止算法。
上述关键点:以一定概率exp(-ΔT/kT) 接受一个不好的解,这是SA区别于爬山算法的地方。

2 SA 算法应用
应用 模拟退火SA 算法求解以下函数的最小值:
y = np.sin(5np.pi(x-0.05)) np.cos(np.pi*(x-0.04)), 0<x<1
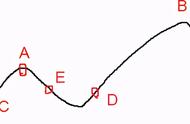
先plot 下函数:

这是有意选取的一个多峰值函数,观察SA算法是否陷入局部极小;爬山算法是怎么陷入局部极小的,SA又是怎么跳出局部极小的。

3 SA 算法代码
代码详细解释 sa函数的参数 y 代表 一元多次函数,后面3个为算法的调节参数,break_cond是连续多少次没有搜索到好解时的跳出条件, k 控制选择概率,step是迭代时步的控制参数。T,T_max 是解空间的取值范围,i 是迭代次数,best是初始最优解,设为在 T处,break_i是控制跳出的次数,每当取到最优解则置为0. 评价函数选用min(s,s').
以下两行是展示搜索过程的代码,不是算法的代码。
save_list.append([T, y(T)])
print('step = %d, T = %f, y = %f' % (i, T, y(T)))