3)提取公共因子并做因子旋转
提取公共因子就是上面提到的求解函数的过程,一般求解方法有:主成分法、最大似然法、残差最小法等等。
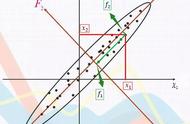
因子旋转的原因是提取公共因子的解有很多,而因子旋转后因子载荷矩阵将得到重新分配,可以使得旋转后的因子更容易解释。常用的方法是方差最大法。
4)对因子做解释和命名
- 目的:解释和命名其实是对潜在因子理解的过程;这一步非常关键,需要非常了解业务才可。这也是我们使用因子分析的主要原因。
- 方法:根据因子载荷矩阵发现因子的特点。
5)计算因子得分
对每一样本数据,得到它们在不同因子上的具体数据值,这些数值就是因子得分。
四、案例讲解数据集介绍:美国洛杉矶2000年街区普查数据,共有110个街区,15个变量,变量具体情况见下表。
想分析影响不同街区下人口分布的潜在因子。

1. 第一步:数据预处理和分析
新增“人口密度”特征,删除特征人口量、面积、经度和维度。
import pandas as pd
import numpy as np
LA_data = pd.read_csv(‘LA.Neighborhoods.csv’)
#新增人口密度,去掉人口量、面积、经度和维度
LA_data[‘density’] = LA_data[‘Population’]/LA_data[‘Area’]
LA_data_final = LA_data.drop([‘Population’,’Area’,’Longitude’,’Latitude’],axis=1)
LA_data_final_feat = LA_data_final.drop([‘LA_Nbhd’],axis=1)

2. 第二步:因子分析——充分性检验
巴特利特P值小于0.01,KMO值大于0.6;说明此数据适合做因子分析。

3. 第三步:因子个数确定
特征值大于1的因子数有2个,且两个因子的累计方差有68%;因此确定因子个数为2个。
from factor_analyzer import FactorAnalyzer
fa = FactorAnalyzer(LA_data_final_feat.shape[1] 1, rotation=None)
fa.fit(LA_data_final_feat)
ev, v = fa.get_eigenvalues # 计算特征值和特征向量
var=fa.get_factor_variance#给出方差贡献率