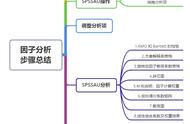
主成分分析和因子分析有什么区别和联系?”这个问题其实很多朋友在后台提问过,今天将这个问题的答案写成推送分享给大家。
方法背景随着硬件技术的发展,每年被记录和存储下来的数据是非常庞大的,如何从庞大的数据堆中筛选出目标数据并分析得到有用的结论是现今重要的领域---数据挖掘。为了能够充分有效的利用数据,化繁为简是一项必做的工作,希望将原来繁多的描述变量浓缩成少数几个新指标,同时尽可能多的保存旧变量的信息,这些分析过程被称为数据降维。
主成分分析和因子分析是数据降维分析的主要手段。另一种化繁为简的手段是聚类。
降维分析简单理解就是将描述事物的众多指标(变量)通过一定的手段浓缩成少数几个有代表性且互不相关的新变量。聚类分析的分析对象是个案,每个个案都会有各种描述其情况的指标,根据各种指标的情况,将个案进行归类。例如,酒店通用的分级标准是一星到五星,每个等级都有对应的很多硬性指标,根据所有指标的综合情况评定酒店的级别。
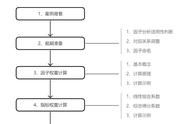
今天我们介绍的就是降维分析的其中两种主要方法:主成分分析和因子分析。
主成分分析主成分分析可以简单的总结成一句话:数据的压缩和解释。常被用来寻找判断某种事物或现象的综合指标,并且给综合指标所包含的信息以适当的解释。在实际的应用过程中,主成分分析常被用作达到目的的中间手段,而非完全的一种分析方法。这也是为什么SPSS软件没有为主成分分析专门设置一个菜单选项,而是将其归并入因子分析。我们可以先了解主成分分析的分析模型。

上面这幅图是经常被用来形象解释主成分分析原理。图中原来有两个坐标轴X1和X2,从散点分布可以很明显的知道散点在这两个坐标轴内存在线性相关。如果将这些散点在坐标轴X1和X2上的取值自变量x1和x2纳入到各种回归模型中,将会由于它们的多元共线问题致使拟合结论出现偏差。那么如何处理才能避免呢?
这里给大家强调,统计学上数据信息往往指的是数据变异(数据波动)。在上图中,散点的分布构成了一个椭圆形点阵,在椭圆的长轴方向,数据波动明显大于短轴方向。此时如果沿着椭圆的长轴和短轴方向设定新的坐标轴(F1和F2)组成坐标系,那么新坐标系可以完全解释数据散点的信息,散点在新坐标轴上的取值就形成两个新的变量(f1和f2),这两个新变量之间是相互独立(不相关)。
从散点图上还可以知道,长轴和短轴能够解释的数据信息是不同的,长轴变量携带了大部分数据的变异信息,而短轴上的变量只携带一小部分变异信息。此时只需要使用长轴方向上的新变量(f1)就可以代表原来两个变量(x1和x2)的大部分信息,达到降维的作用。
主成分分析的这种坐标轴变化是通过将原来的坐标轴进行线性组合完成的。这个线性组合的过程涉及到线性代数部分的内容,这里不过多解释。假设描述对象(例如汽车)由k个自变量指标(油耗、车重、轴长、内饰等等)进行描述,因为这些指标很多都是相关的(重量与油耗),因此可以进行主成分分析,浓缩变量。经过坐标轴线性组合以后,可以形成下面的线性组合式子:

通过线性组合以后,主成分分析可以形成k个新变量。这里的线性组合大家可以理解成原来坐标轴的空间旋转,因此原来有多少变量(k个),经过主成分分析以后,形成数量一致的新变量(k个)。新变量之间的方差关系见下式。通常情况下,我们只许取前面几个即可。

在主成分分析后,SPSS等软件会输出下面这个结果。包括特征根值,方差贡献率和累计方差贡献率。从表格结果可知,原来的变量数量是8个,经过矩阵的线性组合(正交变换)以后,形成了8个成分,前面三个成分总共贡献了数据变异的89.5%,因此提取了前面三个成分作为主成分。