- 特征根是矩阵线性组合后的产物,可以看作主成分的重要性指标,代表引入该主成分后可以解释多少原始变量的信息。如果特征根小于1,说明该主成分的解释力度还不如直接引入一个原变量的平均解释力度大,因此一般可以用特征根大于1作为纳入标准。
- 方差贡献率表示该主成分的方差在全部方差中的比重。这个值越大,表明主成分解释数据信息的能力越强,它与特征根是正相关的,特征根越大,方差贡献率越大。
- 累计贡献率表示前面n个主成分累计提取了多少数据信息。一般来说,如果前k个主成分的贡献率达到85%,表明提取前面k个主成分就基本可以解释所有数据信息。
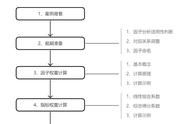
主成分分析的一个重要的结论是主成分矩阵,如下表所示。主成分矩阵可以说明各主成分在原来变量上的载荷,所以也被称为载荷矩阵。

通过载荷矩阵可以写出主成分的组成结构表达式。我们以第一主成分为例,写出其表达式。从式子可以知道,第一主成分包含原来变量X1,X3和X8在信息最多,X2和X7其次,X4,X5和X6更少一些。这就是主成分分析的致命缺陷,提取出来的主成分不能明确解释成某几个原始变量的概率,为进一步分析制造了困难。(这个问题将由因子分析来解决)

主成分分析的另一个结论是主成分得分矩阵。其实就是主成分载荷矩阵除以主成分特征根后得到的矩阵。为什么要除以特征根呢?这是因为主成分载荷矩阵是带有成分重要性属性(包含特征根)的,如果要用提取得到的主成分进行综合排名比较或回归分析,需要先消除主成分的权重不平等(重要性不同),因此需要除以对应主成分的特征根,得到主成分得分矩阵。上表的主成分得分矩阵为:

根据主成分得分矩阵的得分系数,就可以计算每个个案在新变量(主成分)上的数值。进而可以将新变量值用于综合评分和回归。