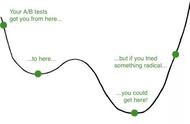
图11 一般共边切割示意图
⑵一笔画共边切割算法。
1)欧拉图与一笔画共边切割。
图论中有一种特殊的欧拉图,它有一条很重要的性质,从欧拉图的任一顶点出发都能求得一条欧拉回路,即可无重复边一笔绘出。其中,如果图中各顶点的度数均为偶数,则图一定是个欧拉图。
另外,如果图中除了某两个顶点(Vi,Vj)的度数为奇数外,其他顶点的度数均为偶数,则一定存在从Vi到Vj的一条路径,它经过了图的各边一次且无重复边,这条路径称为欧拉通路。这个问题不难理解,连接Vi和Vj,补加一条新边,则此时图变成各顶点的度数都是偶数,即构成了欧拉回路,求得欧拉回路后,再去掉Vi与Vj间补加边,即得到Vi到Vj的欧拉通路。显然欧拉通路也仅需一个打孔点且一次切割中无空行程,因此我们可以利用欧拉图的原理对共边排样零件进行共边切割。对于欧拉图由于割嘴只需打一次孔,所以对这种方法的共边切割简称一笔画共边切割。
2)一笔画共边切割实现举例。
如图12所示,是一个欧拉图它可以无重复边一笔绘出,其遍历轨迹为:1→2→3→4→2→5→3→6→7→4→1。
如图13所示,为一个简单的非欧拉图添加虚边的过程。

图12 欧拉图的遍历轨迹

图13 非欧拉图添加虚边方法
对于非欧拉图虚边添加的引入,便可以提出一种能满足共边切割的欧拉回路的求解方法。
⑶“阶梯型”共边切割方法。
1)“阶梯型”数学模型。
设矩形阵列为m行n列,则共有m×n个矩形零件,第i行第j列的零件可表示为Pij(i=1,2,… m;j=1,2,… n)。如果零件Pij有任一个边被切割,则记c(Pij)=1,否则c(Pij)=0,未切割状态下所有零件c(Pij)=0。实现的目标为切割完m×n个零件所需要的切割次数小于等于m×n,且越小越好。
2)“阶梯型”共边切割算法实现。
①第一次打孔首先切割掉零件P11,则与零件P11有公共边的零件P12和P21都有一条边被切割,因此记c(P12)=1,c(P21)=1。记m×n个矩形零件的集合为A,切割的零件集合记为B,则剩余的零件集合为C=A-B。
②在剩余的零件集合C中找出c(Pij)=1的所有零件,记为集合T。
③在集合T中选出零件下标列序号最小的零件Pij,以零件Pij的顶点为起点,确保按照阶梯形的轨迹打一次孔就能把集合T中的所有零件切割完毕。
④重复②和③直到剩余集合C中的零件为空。
现在给出一个实例,如图14所示,这是一些矩形的阵列排列组成的共边排样图,按照算法步骤,我们可得到最终切割轨迹为: