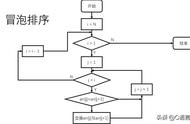
总共执行N-1次操作,所有元素归位。
3.4
代码实现
for(inti=0;i<n-1; i){
for(intj=0;j<n-i-1; j){
if(a[j]>a[j 1]){
swap(a[j],a[j 1]);
}
}
}
04
问题及优化
4.1
迭代轮次优化
如果原数组为如下情况,那么在执行完第1轮后,整个数组已经有序,后面的轮次没必要执行,可以针对这种情况做一次优化改进。
改进点1:
如果某一轮没有发生过交换,说明数组已经有序,那么以后也不会发生交换,此时可以终止迭代。

代码实现
for(inti=0;i<n-1; i){
//flag标记是否有交换
boolflag=true;
for(intj=0;j<n-i-1; j){
if(a[j]>a[j 1]){
swap(a[j],a[j 1]);
flag=false;
}
}
if(flag){
break;
}
}
4.2
扫描范围优化
如果为以下情况,我们会发现最后的6和8所处的位置和最终排序完成的位置一样,说明过程中他们的位置不会发生变化。

上一轮最后交换的位置,在下一轮时,此位置后面的数也不会再发生交换。

改进点2:
记录每一次最后发生交换的位置,下一轮只需要扫描到此位置的前一个即可。
代码实现
//记录最后交换的位置
intposition=0;
intlen=n-1;
for(inti=0;i<n-1; i){
//flag标记是否有交换
boolflag=true;
for(intj=0;j<len; j){
if(a[j]>a[j 1]){
swap(a[j],a[j 1]);
flag=false;
position=j;
}
}
len=position;
if(flag){
break;
}
}
05
总结
冒泡排序是比较简单的一种排序算法,核心思想就是比较相邻的两个数,但效率比较低所以可做一些优化。时间复杂度为O(N^2),数据规模较小时可采用,但数据过大时就不建议采用冒泡了。
来源:小K算法
作者 :小K
原标题:图解算法:冒泡排序
编辑:hxg、yrLewis