如果需要查看排版好看的请搜索微信公众号放开我我还能学
前言
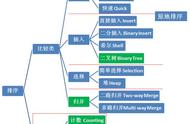
这次我们介绍交换类排序中的冒泡排序,和简单插入排序相似,冒泡排序虽然时间复杂度也是O(n^2),但是对于有序数组的排序,时间复杂度也可以降为O(n),效率是比较高的。
冒泡排序
对数组[1, 4, 3, 2, 5, 6, 7, 8]从小到大排序,使用冒泡排序步骤如下:
- 依次比较相邻元素的大小。
- 如果前面的数据大于后面的数据,就交换这两个数据,然后向右移动一步,接着比较。经过第一轮的多次比较交换后,最大的数据就移动到了最后。
- 以此类推,经过 n 轮循环,数组就排序好了。
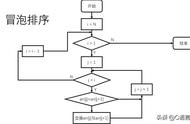
下图展示了冒泡排序的过程:

冒泡排序代码:
public static void sort(Comparable[] arr) {
int n = arr.length;
for (int i = n; i > 0; i--) {
for (int j = 1; j < i; j ) {
if (arr[j - 1].compareTo(arr[j]) > 0) {
swap(arr, j - 1, j);
}
}
}
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
优化1
如果对于一个有序的数组,使用上述冒泡排序的话,同样会执行n(n-1)/2次。实际上,在内循环中每一次比较只要没有发生逆序,即元素之间进行交换,那么就说明数组已经有序,这时已经可以退出程序了。
优化思路就是设置一个交换标志swapped,只要发生了交换,就让swapped = true,外部循环判断swapped是否为true,不是就结束程序,说明排序完成。
下面展示了优化思路的过程:

优化代码:
public static void sort(Comparable[] arr) {
int n = arr.length;
boolean swapped = false;
do {
swapped = false;
for (int i = 1; i < n; i ) {
if (arr[i - 1].compareTo(arr[i]) > 0) {
swap(arr, i - 1, i);
swapped = true;
}
}
// 每一次for循环将最大的元素放在了最后的位置
// 所以下一次排序, 最后的元素可以不再考虑,n--
n--;
} while (swapped);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
优化2
在上述优化的基础上,我们还可以进一步优化。
对于数组:[1, 4, 3, 2, 5, 6, 7, 8],按照上面的优化思路,我们在第一轮比较时,需要让5, 6, 7, 8比较,第二轮比较时,需要让5, 6, 7比较,然而它们都是有序的排列,因此,我们是否能减少这些不必要的比较呢?答案是可以的。
优化思路就是每一轮循环完后,更新n的值,更新为最后一次交换的位置,这样,在此之后的元素都已经是有序的了,那么下次循环中就不用再比较了。
下图展示了优化思路的过程:

优化代码:
public static void sort(Comparable[] arr) {
int n = arr.length;
int newn;
do {
newn = 0;
for (int i = 1; i < n; i ) {
if (arr[i - 1].compareTo(arr[i]) > 0) {
swap(arr, i - 1, i);
// 记录最后一次的交换位置,在此之后的元素都是已经有序的,因此下一轮扫描中不再考虑
newn = i;
}
}
n = newn;
} while (newn > 0);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}