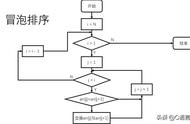
最终执行完上述代码后,arr数组就变成了一个有序的数组。
大家要注意,在上述代码中,bubbleSort方法可以接收一个整数类型的数组arr,通过两层for循环,最终就可以实现整型数组元素的冒泡排序。其中:
- 内层for循环是将相邻的两个元素进行比较。如果不满足左小右大的规则,就将两个元素进行交换。
- 交换相邻的元素时,使用到了临时变量tmp。
- 外层for循环,用来控制需要进行几轮比较,即比较的轮次。
4. 算法总结
通过上述Java程序,我们就实现了冒泡算法的代码实现,最后壹哥再来给大家总结一下冒泡排序算法的时间和空间复杂度等情况。
(1). 冒泡排序的平均时间复杂度是O(n²) 。如果数组本身已经排好了顺序,在优化后的算法中,需要比较n-1次,此时的时间复杂度是O(n)。而当数组是无序的,在优化后的算法中,需要比较的次数是n(n-1)/2次,此时的时间复杂度是O(n²)。
(2). 冒泡排序的空间复杂度为O(1) 。
(3). 冒泡排序是原地排序。
(4). 冒泡排序的重点是左右相邻的两个元素进行两两比较,当两个元素数值相同时不换位,所以是稳定排序。
三. 选择排序1. 概念
选择排序(Selection Sort) 是一种最简单直观的排序算法。即使在我们的日常生活中,大家可能都会经常无意地进行选择排序。比如我们去超市买苹果,你拿了一个袋子,从众多的苹果中挑了一个最大的放入袋中,然后又从剩下的苹果中挑了一个最大的放入袋子。这样如此反复,直到挑够了需要的苹果去结账。这其实就是选择排序的实现思想,就是不断地从未排序的元素中选择最大(或最小)的元素,放入到已排好序的元素集合中,直到未排序的元素为空。
基于上述实现思想,我们就可以提取出选择排序的实现原理:
将一个数组分成有序的区间和无序的区间两部分,初始时有序区间为空,每次从无序区间中选出最小的元素,并放到有序区间的末尾,直到无序区间为空。
2. 实现思路
按照选择排序的实现原理,接下来再把选择排序的实现思路再细化一下:
- 假设,给定一个数组 int[] arr = {n个数据};
- 第1趟排序,在无序数列 arr[0] ~ arr[n-1]中选出最小的数据,将它与arr[0]交换;
- 第2趟,在无序数列 arr[1] ~ arr[n-1]中选出最小的数据,将它与arr[1]交换;
- 依此类推,第i趟在无序数列arr[i]~arr[n-1]中选出最小的数据,将它与arr[i]交换,直到全部排序完成。
但是如何选出最小的一个元素呢?
我们先任意选一个元素,假设它就是最小的元素(默认为无序区间的第一个元素),然后让这个元素与无序区间中的每一个元素挨个进行比较。 如果遇到比自己小的元素,则更新最小值的下标,直到把无序区间遍历完。最后的那个最小值下标对应的数值,就是该无序区间的最小值。
3. 实现步骤
同样的,仍然以一个示例来给大家解释选择排序的实现步骤。假如我们现在有一个待排序的数组[5,8,6,3,9,2,1,7],若采用选择排序算法进行排序,其实现步骤如下:
(1). 初始化待排序数组[5,8,6,3,9,2,1,7];
(2). 从待排序数组中,选出最小值1,和第一个元素5进行交换,即将最小的元素放在下标0的位置上;
(3). 在剩下的无序区间的元素中,选择最小的元素2,并将最小的元素2与无序区间的第一个元素8进行交换。交换后,有序区间的元素变为2个,分别是1和2,剩余的为无序区间。
(4). 依次类推,将所有的元素通过不断选择的方式,按有序的方式放到有序区间,最终把整个数组全部排好顺序。
我们把上述选择排序的文字描述内容,变成对应的图片,会如下图所示: