这篇文章我们共同学习狄克斯特拉算法,我们都知道狄克斯特拉算法的目的是找出图中的最短路径,那相比于广度优先搜索算法来说,广度优先搜索算法只是找到了从起点到达终点所经过的段数最少,但不一定是最快的路径,通俗点讲就是折腾次数是最少的,就像从西安回浙江,我们可以乘坐高铁再转飞机,也可以开车直接过去。但开车一定不比不过高铁飞机的时间,但显然是最不折腾人的路径。那么我们应该如何找出这个时间最短的路径呢?狄克斯特拉算法回答了这一问题。

狄克斯特拉
狄克斯特拉算法原理

路径描述
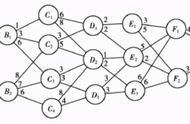
其中数字代表时间,单位是分钟,如果要找到从起点到终点的耗时最短的路径,那么我们可以使用狄克斯特拉算法。
狄克斯特拉算法四步走:
1、 先找出最短时间到达的节点(起点开始)
2、 更新该节点的邻居节点的开销
3、 重复第2步,直到终点
4、 计算最短路径
接下来我们就应用这四步详细看一下
第一步:先找出最短时间到达的节点。从起点开始,我们可以到达A点,也可以到达B点,由图可知,到达A点需要6分钟,而到达B点只需要2分钟,那么我们从起点走向B点,记录时间为2分钟。
第二步:更新该节点的邻居节点的开销。从B点可以到达A点,也可以直接到达终点,但不一定直接到终点就是时间最短的路径。因此我们得到点B到达A点是3分钟,到达终点的时间是5分钟,注意计算的还是所用的总开销,因此到达A点的开销变成2 3=5分钟,到达终点的时间是2 5=7分钟,还需注意从起点直接到达A点的时间是6分钟,显然比起点到B点到A点的时间还
要长,那么我们可以确定出我们的路径是起点—>A点—>B点,用时5分钟。
第三步:重复第二步。现在我们到达了A点,更新A点的邻居节点开销。从A点到达B点,A点到达终点,单向表示我们不走回头路,我们可以直接到达终点,用时1分钟,总时间为5 1=6分钟。
第四步:确定最短路径。起点—>B点—>A点—>终点。
那么如果我们采用广度优先搜索算法,最短路径并不是这一条,那是哪条呢?留给读者你们看吧……
专业术语
上面所说的时间或者开销用计算机专业术语称为权重,带权重的图称为加权图,不带权重的图称为非加权图。计算加权图的最短路径,使用狄克斯特拉算法;计算非加权图的最短路径,可以使用广度优先搜索算法。

佛系算法
- 狄克斯特拉算法代码实现:
public class Dijkstra {
//设置没有已知到达路径的标记
private static int NOWAY_SIGN = Integer.MAX_VALUE;
private static final String START = "start";
private static final String END = "end";
public void getMinStep(String start, String end, Map<String, Map<String, Integer>> graph) {
//各节点的最少花费
Map<String, Integer> costs = graph.get(start);
//各节点最少花费时的父节点
Map<String, String> parents = new HashMap<String, String>();
//已处理的节点
HashSet<String> processed = new HashSet<String>();
//在未处理的节点中找到开销最小的节点
String node = findLowestCostNode(costs, processed);
while (node != null && graph.get(node) != null) {
int cost = costs.get(node);
//遍历当前节点的所有邻居
Iterator iterator = graph.get(node).entrySet().iterator();
while (iterator.hasNext()) {
Map.Entry<String, Integer> entry = (Map.Entry) iterator.next();
//通过node节点到该节点的最小消耗
int newCost = cost entry.getValue();
//更新从start到该节点的最小消耗
if (!costs.containsKey(entry.getKey()) || costs.get(entry.getKey()) > newCost) {
costs.put(entry.getKey(), newCost);
parents.put(entry.getKey(), node);
}
}
//该节点加入已处理
processed.add(node);
//找出当前最小消耗的节点
node = findLowestCostNode(costs, processed);
}
printPath(parents, costs.get(END));
}
public void initParents(String start, Map<String, Integer> startGraph, Map<String, String> parents) {
Iterator iterator = startGraph.entrySet().iterator();
while (iterator.hasNext()) {
Map.Entry<String, Integer> entry = (Map.Entry) iterator.next();
parents.put(entry.getKey(), start);
}
}
/**
* 找出未处理节点中消耗最小的节点
*
* @param costs
* @param processed
* @return
*/
public String findLowestCostNode(Map<String, Integer> costs, HashSet<String> processed) {
int lowestCost = NOWAY_SIGN;
String lowestCostNode = null;
Iterator iterator = costs.entrySet().iterator();
while (iterator.hasNext()) {
Map.Entry<String, Integer> entry = (Map.Entry) iterator.next();
if (!processed.contains(entry.getKey()) && entry.getValue() < lowestCost) {
lowestCost = entry.getValue();
lowestCostNode = entry.getKey();
}
}
return lowestCostNode;
}
public void printPath(Map<String, String> parents, int cost) {
Stack<String> stack = new Stack<String>();
String parent = parents.get(END);
while (parent != null) {
if (START.equalsIgnoreCase(parent)) {
stack.push(START);
break;
}
stack.push(parent);
parent = parents.get(parent);
}
StringBuffer path = new StringBuffer();
while (!stack.empty()) {
String node = stack.pop();
if (path.length() != 0) {
path.append("->");
}
path.append(node);
}
System.out.println("最优路线:" START "->" path.toString() "->" END);
System.out.println("其开销为:" cost);
}
public static void main(String[] args) {
Map<String, Map<String, Integer>> graph = new HashMap<String, Map<String, Integer>>();
Map<String, Integer> start = new HashMap<String, Integer>();
start.put("A", 5);
start.put("B", 2);
graph.put(START, start);
Map<String, Integer> a = new HashMap<String, Integer>();
a.put("C", 4);
a.put("D", 2);
graph.put("A", a);
Map<String, Integer> b = new HashMap<String, Integer>();
b.put("A", 8);
b.put("D", 7);
graph.put("B", b);
Map<String, Integer> c = new HashMap<String, Integer>();
c.put("D", 6);
c.put(END, 3);
graph.put("C", c);
Map<String, Integer> d = new HashMap<String, Integer>();
d.put(END, 1);
graph.put("D", d);
Dijkstra dijkstra = new Dijkstra();
dijkstra.getMinStep(START, END, graph);
}
}