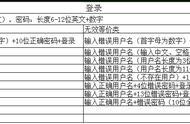
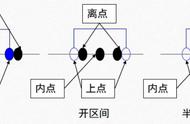
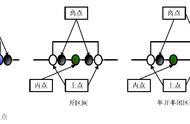
图5-3 因果图的基本图形符号
① 恒等:若原因出现,则结果出现;若原因不出现,则结果也不出现。
② 非(~):若原因出现,则结果不出现;若原因不出现,则结果出现。
③ 或(∨):若几个原因中有1个出现,则结果出现;若几个原因都不出现,则结果不出现。
④ 与(∧):若几个原因都出现,结果才出现。若其中有1个原因不出现,则结果不出现。
为了表示原因与原因之间、结果与结果之间可能存在的约束条件,在因果图中可以附加一些表示约束条件的符号。从输入(原因)考虑,有4种约束,例如:(a)、(b)、(c)、(d)。从输出(结果)考虑,还有1种约束,例如:(e),如图5-4所示。

图5-4 因果图的约束符号
① E(互斥):表示a、b两个原因不会同时成立,两个中最多有一个可能成立。
② I(包含):表示a、b、c这3个原因中至少有一个必须成立。
③ O(惟一):表示a和b当中必须有一个,且仅有一个成立。
④ R(要求):表示当a出现时,b必须也出现。a出现时不可能b不出现。
⑤ M(屏蔽):表示当a是1时,b必须是0。而当a为0时,b的值不定。
2.因果图测试用例
例如:有一个处理单价为1元5角钱的盒装饮料的自动售货机软件。若投入1元5角硬币,按下“可乐”、“雪碧”或“红茶”按钮,相应的饮料就送出来。若投入的是两元硬币,在送出饮料的同时退还5角硬币。
分析这一段说明,我们可以列出原因和结果。
原因:① 投入1元5角硬币;② 投入2元硬币;
原因:③ 按“可乐”按钮;④ 按“雪碧”按钮;⑤ 按“红茶”按钮。
中间状态:① 已投币;② 已按钮。
结果:① 退还5角硬币;② 送出“可乐”饮料;
原因:③ 送出“雪碧”饮料;④ 送出“红茶”饮料。
根据原因和结果,我们可以设计这样一个因果图(如图5-5所示。)

图5-5 因果图
转换为测试用例,如表5-6所示,每一列可作为确定测试用例的依据。
表 5-6
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |||
输 入 | 投入1元5角硬币 | (1) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
投入2元硬币 | (2) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
按“可乐”按钮 | (3) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |
按“雪碧”按钮 | (4) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
按“红茶”按钮 | (5) | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
中间 结点 | 已投币 | (11) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
已按钮 | (12) | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
输 出 | 退还5角硬币 | (21) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
送出“可乐”饮料 | (22) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
送出“雪碧”饮料 | (23) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
送出“红茶”饮料 | (24) | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
2.6 判定表驱动法
前面因果图方法中已经用到了判定表。判定表是分析和表达多逻辑条件下执行不同操作的情况的工具。在程序设计发展的初期,判定表就已被用作编写程序的辅助工具了。它可以把复杂的逻辑关系和多种条件组合的情况表达得较明确。
1.判定表组成
判定表通常由4个部分组成,如图5-6所示。

图5-6 判定表
条件桩(condition stub):列出了问题的所有条件。通常认为列出的条件的次序无关紧要。
动作桩(action stub):列出了问题规定可能采取的操作。这些操作的排列顺序没有约束。
条件项(condition entry):列出针对它所列条件的取值,在所有可能情况下的真假值。
动作项(action entry):列出在条件项的各种取值情况下应该采取的动作。
规则:任何一个条件组合的特定取值及其相应要执行的操作。在判定表中贯穿条件项和动作项的一列就是一条规则。显然,判定表中列出多少组条件取值,也就有多少条规则,条件项和动作项就有多少列。
2.判定表建立
判定表的建立因该依据软件规格说明,步骤如下:
① 确定规则的个数。假如有n个条件,每个条件有两个取值(0,1),故有2n种规则。
② 列出所有的条件桩和动作桩。
③ 填入条件项。
④ 填入动作项。制定初始判定表。
⑤ 简化。合并相似规则或者相同动作。
Beizer指出了适合使用判定表设计测试用例的条件:
① 规格说明以判定表的形式给出,或很容易转换成判定表。
② 条件的排列顺序不影响执行哪些操作。
③ 规则的排列顺序不影响执行哪些操作。
④ 当某一规则的条件已经满足,并确定要执行的操作后,不必检验别的规则。
⑤ 如果某一规则要执行多个操作,这些操作的执行顺序无关紧要。
2.7 正交试验法
利用因果图来设计测试用例时,作为输入条件的原因与输出结果之间的因果关系,有时很难从软件需求规格说明中得到。往往因果关系非常庞大,导致利用因果图而得到的测试用例数目多得惊人,给软件测试带来沉重的负担。为了有效地、合理地减少测试的工时与费用,可利用正交试验法进行测试用例的设计。
1.正交试验设计方法
依据Galois理论,正交试验设计方法是从大量的试验数据中挑选适量的、有代表性的点,从而合理地安排测试的一种科学的试验设计方法。
正交试验法,就是使用已经造好了的表格“——”正交表来安排试验并进行数据分析的一种方法。它简单易行并且计算表格化,应用性较好。下边通过一个例子来说明正交试验法。
例题:为提高某化工产品的转化率,选择了三个有关因素进行条件试验,反应温度(A),反应时间(B),用碱量(C),并确定了它们的试验范围如下。
A:80~90℃;
B:90~150分钟;
C:5%~7%。
试验目的是搞清楚因子A、B、C对转化率有什么影响,哪些是主要的,哪些是次要的,从而确定最适生产条件,即温度、时间及用碱量各为多少才能使转化率最高。这里,对因子A、B和C,在试验范围内都选了三个水平,如下所示。
A:A1=80℃,A2=85℃,A3=90℃;
B:B1=90分钟,B2=120分钟,B3=150分钟;
C:C1=5%,C2=6%,C3=7%。
当然,在正交试验设计中,因子可以是定量的,也可以是定性的。而定量因子各水平间的距离可以相等,也可以不相等。这个三因子三水平的条件试验,通常有两种试验方法:
① 取三因子所有水平之间的组合,即A1B1C1,A1B1C2,A1B2C1,……,A3B3C3,共有33=27次试验。用图5-7表示立方体的27个节点。这种试验法叫做全面试验法。