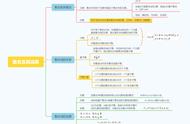
第一步:写中括号{};
第二步:划竖线{丨};
第三步:竖线左边是表示这个集合元素的一般符号及取值范围,右边是这个集合中元素的共同持征。
[关键]
1、竖线“丨”左边字母是任意的,但一般有约定俗成的符号。
例:{Ⅹ丨Ⅹ>0}与{y丨y>0}是同一个集合。因为它表示的是大于0的元素组成的集合,用字母x、y、m……表示都一样。但集合{X丨y=X^2 1}与集合{y|y=X^2 1}是两个不同的集合。前者表示集合的基本元素X的属性是函数y=X^2 1的定义域,即Ⅹ的取值范围,是R。后者表示集合的基本元素y的属性是函数y=X^2 1的值域,是y的取值范围,是不小于1的实数。这里“X”与“y"不能写错。
2、竖线“丨"左边字母取值范围当X∈R时常常省略不写,如上例。但有时候是不能省略的。如
{X∈R丨X>0}与{X∈Z|X>0}就是两个不同的集合。前者是由正实数组成的集合,后者是由正整数组成的集合。
3、竖线“丨”左边表示集合的元素的一般符号有这几个形式:
①{X|y=X^2 1}
②{y丨y=X^2 1}
③{(x,y)丨y=X^2 1}
①②前面已说明,③表示由抛物线y=X^2 1图象上所有的点组成的集合。
上面3个都是用描述法表示的集合,尽管竖线“丨”后面的方程相同,但它们是不同的集合,这是由竖线“丨"前面表示集合里元素的一般符号确定的。
再看下面集合,与上面3个比较一下:
④{m∈R丨S=m^2 1};
⑤{S∈R丨S=m^2 1};
⑥{(m,S)丨S=m^2 1}
它们有什么关系?