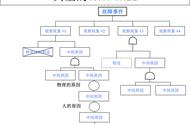
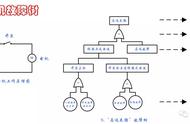
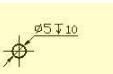
三、失效率和累计失效概率
在进行FTA的定量分析中,常常涉及失效率和累计失效概率。失效率,通常也指故障率,累计失效概率,有时也称故障概率,这两者在进行FTA的定量分析中,极易混淆,现对两个概念进行说明。
失效率,到某时刻尚未发生故障(失效)的产品,在该时刻后单位时间内发生故障(失效)的概率,称为产品的失效率,失效率一般用λ(t)表示,计算见公式(1)所示。

式中:
Δr(t)——t时刻后,Δt 时间内发生故障的产品数;
Δt ——所取时间间隔;
NS(t)——在t时刻没有发生故障的产品数。
累计失效概率,又称不可靠度,是指系统(或设备、产品)在规定的条件、规定的时间t内丧失规定功能的概率,写做F(t),计算见公式(2)所示。

式中:
n(t)——从开始工作(t=0)到任意时刻t,产品的失效数;
N——产品总数。
指数分布是可靠性工程中较为重要的一种分布,当产品工作进入“浴盆曲线”的偶然故障期后,产品的故障率基本接近常数,故障率呈现一种“无记忆性”,此时λ(t)=λ,可得产品的累计失效概率函数见公式(3)。

四、故障树定量计算
使用下行法得到某医疗设备“图像输出异常”最小割集:K1={X1 },K2={ X2},K3={X3},K4={X4},K5={ X5 },K6={ X6 }。各个底事件失效率统计见表2所示。