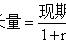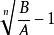增长率属于公务员行测资料分析部分的考点,包含内容众多,主要包括增长率、百分数与百分点、增长率与倍数、成数与翻番、增幅、降幅与变化幅度、增长率比较等方面的内容,今天给大家具体进行相关内容介绍,还整理了相应的练习题,赶紧学习起来吧。

▲增长率
(一)含义
增长率是表述基期量与现期量变化的相对量。增长率又称增速、增幅或者增长幅度、增值率等,增长率为负时表示下降。
(二)增长率、降幅、变化幅度的区别
(1)增长率:有正有负,比较时带符号→ 5% > -10%。
(2)降幅:必须为负,比较时看绝对值→ |-5%| < |-10%|。
(3)变化幅度:有正有负,比较时看绝对值→ |5%| < |-10%|。
◆例:在增长率 10%、-20%、30%、40%、-50%、-60% 中:
①增长率最大的是:40%。先排除负的,-20%、-50%、-60%排除;再从剩下的中挑最大的,为 40%。
②降幅最大的是:-60%。必须为负,先排除 10%、30%、40%,剩下的找绝对值最大的,则降幅最大的是 -60%。
③变化幅度最大的是:-60%。可正可负,看绝对值最大的,为 -60%。
(三)公式:
r= 增长量 / 基期(核心公式)= 增长量 /(现期 - 增长量)(常考 1)
=(现期 - 基期)/ 基期(常考 2)
(四)速算——截位直除
(1)除前看最接近的选项之间的差距。
(2)差距大,截两位。
差距大:①首位不同;②首位相同,次位差大于首位。
(3)差距小,截三位。
(4)截位原则:看下一位(保留两位看第三位、保留三位看第四位),四舍五入。
(5)一步除法,截分母。
(6)多步除法,截分子、分母。
(7)如果选项之间有 10 倍左右的关系,需要看小数点、位数、单位。

▲百分数与百分点
(一)含义
(1)百分数:用来反映量之间的比例关系。
(2)百分点:用来反映百分数的变化。
(二)百分数、百分点的区别
百分数表示两个量的比例关系,用除法计算;百分点表示百分数的变化,用加减法计算。
比如:问 10% 比 4% 多多少,两个百分数之间用百分点来描述,用加减法,10%-4%=6%,数值上是 6%,但表述的时候是 6 个百分点。
◆例:(2019 联考)2017 年我国成年国民图书阅读率为 59.1%,比上年增加 0.3 个百分点;报纸阅读率为 37.6%,比上年降低 2.1 个百分点。
① 2016 年我国成年国民图书阅读率为:遇到“增加”用减法,59.1%-0.3%=58.8%。
② 2016 年我国报纸阅读率为:遇到“降低”用加法,37.6% 2.1%=39.7%。
▲增长率与倍数
(一)增长率:
1. 识别:
增长 比例(相对量,比如百分数、倍数、成数),又名:增速、增幅、增值率。
2. 公式:增长率 =(现期 - 基期)/ 基期。
(二)倍数:
1. 识别:A 是 B 的几倍,A 比 B 多几倍。
2. 公式:是几倍 =A/B,比如问 500 是 100 的几倍,500/100=5。多几倍(增长率)=(A-B)/B=A/B-1,其中,A/B 就是“是几倍”,多几倍 = 是几倍 -1。
比如:问 500 比 100 多几倍,(500-100)/100=4。
(三)两者关系
倍数 = 增长率 1。(A-B)/B 与(现期 - 基期)/ 基期的形式是一样的,说明多几倍 = 增长率。r= 是几倍 -1,则是几倍 =r 1。
比如:2019 年比 2018 年增长了 50%,问 2019 年是 2018 年的几倍,1 50%=1.5 倍;2018 年比 2017 年增长了 20%,则 2018 年是 2017 年的 1 20%=1.2 倍。
◆例:(2017 国考)某市 2015 年全年粮食总产量 4.16 万吨,同比下降 2.3%;甘蔗产量 0.57 万吨,下降 23.6%;油料产量 0.12 万吨,增长 32.4%。问:甘蔗产量是油料几倍?甘蔗产量比油料多几倍?
※ 答:甘蔗产量是油料的 0.57/0.12 ≈ 5 倍。甘蔗产量比油料多 5-1=4 倍。
▲成数与翻番
(一)成数
几 成 就 相 当 于 十 分 之 几, 也 就 是 百 分 之 几 十。 比 如 1 成 =1/10=10%。3 成=3/10=30%。
(二)番数
1. 识别:翻了几番。
2. 一句话:遇番数,化倍数,翻 N 番,变为原来的 2N 倍。翻 1 番,变为原来的 2 倍,翻 2 番,变为原来的 4 倍,翻 3 番,变为原来的 8 倍,翻 4 番,变为原来的 16 倍,2=21,4=22,8=23,16=24,底数都为 2,番数跟指数是对应的,因此翻 N 番,变为原来的 2N 倍。
◆例:2018 年某省国民生产总值为 250 亿元,到 2025 年要达到国民生产总值翻 4 番的目标,问:2025 年的国民生产总值的目标为多少亿元?
※ 答:翻 4 番为 24=16 倍,250×16=4000 亿元。
▲增幅、降幅与变化幅度
(1)增幅一般就是指增长率,有正有负。
(2)降幅指下降的幅度,比较降幅的大小时,只比较绝对值(正增长率不参与降幅的比较)。
(3)变化幅度指增长或下降的绝对比率,变化幅度比较大小时用增长率的绝对值。
◆例:(1)2017 年收入 10 万元,同比增长 10%,增速比去年提高 5 个百分点,则2016 年的增长率为多少?
※ 答:出现“提高”,用减法,10%-5%=5%。
(2)2017 年收入 10 万元,同比增长 10%,增速比去年回落 5 个百分点,则 2016 年的增长率为多少?
※ 答:出现“回落”,用加法,10% 5%=15%。
(3)2017 年收入 10 万元,同比下降 10%,降幅比去年扩大 5 个百分点,则 2016 年的降幅为多少?增长率为多少?
※ 答:下降 10% 为 -10%,降幅比去年扩大 5 个百分点,降幅计算时不带符号,10%-5%=5%,即 2016 年降幅为 5%,增长率为 -5%。
(4)2017 年收入 10 万元,同比下降 10%,降幅比去年收窄 5 个百分点,则 2016 年的降幅为多少?增长率为多少?
※ 答:降幅为 10% 5%=15%,增长率为 -15%。
记忆口诀:“增速”→高减低加。“降幅”→ -(高减低加)
▲增长率比较
(一)识别:
增速最快 / 最慢、增长幅度最大 / 最小。
(二)题型:
已知现期、基期,比较增长率→ r=(现期 - 基期)/ 基期 = 现期 / 基期 -1。比较的时候,如果是 A/B-1 和 C/D-1,都有“-1”,可以直接比较 A/B 和 C/D 的大小。
(三)方法:
看现期和基期的倍数关系是否明显。
(1)当现期 / 基期 =1 (不明显),用(现期 - 基期)/ 基期比较。
(2)当现期 / 基期 =2 (明显),用现期 / 基期比较。
◆例:下图(2012-2015)哪一年的同比增速最快?

※ 答: 图 中 看 倍 数 关 系 明 不 明 显,2011 年 跟 2012 年 倍 数 关 系 明 显, 直 接 用426/133=3 ,866/426=2 ,1600/866=1 ,1800/1600=1 ,明显 2012 年增速最大。