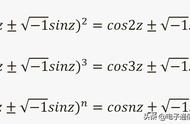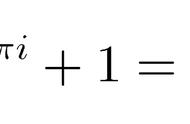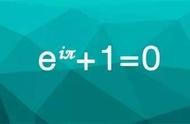真的,这也是欧拉公式。
虽然我们称之为欧拉公式,但第一个证明欧拉公式成立的却是Descartes(笛卡尔),而后才轮到欧拉。但第一个真正给出严格证明的则是20岁的柯西。
来自百度百科的证明过程:从多面体去掉一面,通过把去掉的面的边互相拉远,把所有剩下的面变成点和曲线的平面网络。不失一般性,可以假设变形的边继续保持为直线段。正常的面不再是正常的多边形即使开始的时候它们是正常的。但是,点,边和面的个数保持不变,和给定多面体的一样(移去的面对应网络的外部。)


抱歉,实在没法读懂百度百科的这段解释,如果有模友能解释清楚的记得留言,另外也去百度百科把这段内容修改一遍。
既然没办法像欧拉、柯西这般数学家那样去思考这个问题,不聪明的超模君只能按照最笨的方式,一个一个多面体来计算。

(脑子正在加载.gif)