高一阶段三角函数既是重点又是难点,需要记忆的基础知识与公式很多,特别是恒等变换的公式,是许多学生心中的痛。
如果能够知其然并知其所以然,则能大大降低记忆的难度。
下面看看人教版教材是如何证明cos(α-β)的公式的。
2019人教A版cos(α-β)的推导思路
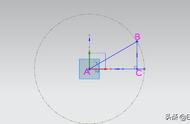
1 在平面直角坐标系中作单位圆,作出角α、β和(α-β),标出各角终边与单位圆的交点坐标;
2 利用扇形的旋转及圆的旋转对称性得到弧相等及弦相等;
3 利用两点间的距离公式建立角及三角函数值的等量关系;
4 化简得到cos(α-β)恒等式。



2019人教B版cos(α- β)的推导思路
其核心是利用了向量的数量积
1 在平面直角坐标系中作单位圆,作出角α、β,标出各角终边与单位圆的交点坐标;
2 利用向量数量积的定义和坐标运算建立角及三角函数值的等量关系;
3 化简得到cos(α-β)恒等式。


证得cos(α-β)=cos(α)cos(β) sin(α)sin(β),令β=-β,结合诱导公式可得cos(α β)。
取β=β π/2,结合诱导公式可得sin(α-β),同理可得sin(α β)。
在此基础上可得到tan(α β)、tan(α-β)及倍角等一系列公式。
,