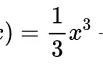这就是一个线性变换,从左边的f(x),变到了,右边的a0,a(n),b(n)。而3个变换积分,就是线性代数中的“矩阵”!细品!
这里要非常地岔开一下!!!
我们从初中收到的教育,y=f(x),就是y是x的函数,就是映射。这个对学FT是一个非常大的阻碍。导致总觉得FT非常不自然。一个函数居然能成为一系列正弦函数的和?!非常地匪夷所思。这个思想的根本问题在于,你还是站在初等数学的角度,或者说站在古典微积分的角度看函数这个概念。函数是x到y的映射。
就像你站在伽利略变换的角度,永远无法理解狭义相对论。你站在均匀空间的角度,永远无法理解广义相对论,一样。
抛弃函数这个概念!欲练神功,挥刀自宫!一切都是级数!一切都是无穷和!
在级数的眼里,任何东西都是一串有规律的表达式的和,无穷和!我们借用信号系统里,冲激函数的概念

明白了?即便在传统意义上的函数,我们依然可以看成一系列有规律的表达式的和,这里就是一串冲激函数的和,只不过每个冲激函数都被调制了!在线性代数的角度,冲激函数就是基,而且是标准的不能再标准、简单的不能再简单的,正!交!基!
那么三角级数,就是原本你是用冲激函数这组基线性组合的,现在我用三角函数这组基来搞线性组合,不可以吗?站在线性代数的角度,当然可以!而且无比自然!
所以,学FT,首先要破除这个我们学了中学6年的函数的思想。将y=f(x),不要看成一个表达式。充分理解了这点。那么接下来的问题就是:
既然x能描述y,肯定不止x能描述y,能找到其他的表达式就行。
这就是线性代数的思想——空间变换!就是找到另一组正交基!这里,由于三角函数系的正交性,自然而然就被我们选中!
稍微总结一下,体会一下,再继续后面的推导过程!
总之,在级数的宇宙观里,没有映射这个玩意儿。一切都是无穷和。加点线性代数的概念,一切都是一组无限维数的正交基的线性组合。充分理解这个观点,直到你对
0.999999.... = 1
有了新的认识。
4 三角级数的推导接着就是形而下的问题了,如何求系数。
在线性代数角度看,就是求解一个非常“稠密的”线性方程组。
码字太烦,直接上图

以上就是傅里叶级数的三角级数形式。
5 傅里叶级数的复数形式教材中,包括信号系统的教材,把复数形式的傅里叶级数,用欧拉公式,从三角级数推导。这个方法非常烂!
如果你充分理解了上面的过程。应该有一个问题:还有没有其他的级数?或者站在线性代数的角度,还有没有其他空间了?或者有没有其他的正交基了?舔狗地讲,哪怕不正交也行。答案是有的,女神可不只三角函数一个!指数函数也可以组成正交基

这里一个小问题是,为什么指数函数可以有负数部分了?原因还是在于正交性!
三角函数中,由于负部分对三角函数构成冗余,导致基的非正交,所以我们舍弃了负的部分。而在指数函数中,如果要构成正交,必须引入负的部分。
接下去就可以用三角级数的过程,定积分的思想,推导复数级数。这里略。
用这个思路去理解所谓的“傅里叶级数的复数形式”!或者抛弃“傅里叶级数”、“傅里叶级数的复数形式”两个名词。着眼于“三角级数”、“复指数级数”两个名词,或许更能说明问题。
将欧拉公式看成一种偶遇,正好指数函数是三角函数的复数形式。假装我们发现了新的正交基(复指数),并又满怀豪情地推导了一把。
6 傅里叶变换微积分中,对傅里叶变换的描述非常少,甚至于标题都是傅里叶积分。直接上图