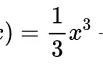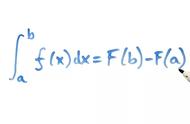本篇将傅里叶变换,下面以FT简称。
网上有很多关于FT的文章,还有动画,一系列首尾相连的棍子,甩啊甩。看着狂拽酷炫,然并卵,看完了觉得FT很牛逼,但依然不明白FT。怎么一个好端端的函数,就是一系列正弦波了?什么时域频域,听着高大上。
本文从最基本的三角级数开始,阐述FT的数学本质。内容非常硬核,如果只想随便看看,搜搜FT的视频,看看甩甩小棍子的即可。
0 序,为什么FT这么难以理解FT在微积分中放在最后一章的最后一节,本身来讲篇幅不多,概念、定理、推导过程都不多,只是开了个头。之后,FT在信号与系统中出现。但是,信号系统中,着重FT的应用。对FT的导出并不是它的重点。所以就FT的学习来讲,是脱节的。微积分中不谈FT的应用,导致FT的意义没有很好落实。信号系统中FT的导出又是不够严谨的,导致知其然不知其所以然。而FT的思想,微积分教材本身是不阐明的。所以,这就造成了对于每个工科学生来讲,FT就是噩梦,稀里糊涂的睡,稀里糊涂的醒。
我们学FT,必须把各科的教材对应看。光看一册是不够全面的,自然无法体会FT的奥义。
首先:
- FT推导在于微积分,因为用到了定积分的概念,这是形而下。
- FT理解于线性代数,它的数学本质是线性空间的变换,这是形而上。
- FT应用于信号系统,这是形而下中下。
明白了这三点,学习FT就有了路。
其次,学FT,必须学它的根基。把基础打扎实。FT的基础是傅里叶级数,傅里叶级数的基础是三角级数。所以,至少我学FT,一半以上的精力是花在三角级数。弄明白了三角级数的来龙去脉,FT是水到渠成的东西。
1 级数讲三角级数前,还是得先回顾一下级数。级数是个好东西,它能把不好的变成好的。比如幂级数,一个非常好的用处就是能解方程,无论是超越方程还是微分方程。电路中,整流电路就是靠泰勒级数求解的。
级数又是一个非常反直觉的概念。举几个例子。首先就是大家耳熟能详的
0.9999999999.... = 1
再来一个,条件收敛的常数项级数,调换项,可能导致级数不收敛,也可能导致收敛到其它值。简单来讲就是条件收敛的级数不符合加法交换律。乍一看非常神奇!从小学学起的加法交换律居然不成立了!
微积分中,级数还是一个非常重要的概念和理论。它能证明好多教材在前面中埋下的坑。如,如何判断隐函数有函数,如何判断微分方程有解,甚至有唯一解。
形式上来讲,级数就是无穷个有规律的项的和。所以,我们可以用任何组合,只要有规律的,都可以替代数或者函数。而剩下两个问题:
- 是否收敛于常数或者函数,(废话,不收敛的要来干啥)
- 收敛速度,(当然越快越好)。
问题1,工科有福了,可以不管,有狄利克雷收敛条件保证。万一不满足,不要紧,有广义FT。
问题2,FT不涉及。
2 三角级数为什么函数要转换成三角级数?这恐怕是第一个问题,暂且按下。我们要解决的是,如果表示成三角函数的级数,怎么个形式?
下面是第一个想到的:

非常自然,但也是非常不好的。因为它不正交。不正交的问题在于非常难求系数。所以化成:

这个形式非常好,正交!非常容易求系数。
什么是正交,为什么正交是我们追求的,看下面的推导过程。
随之而来的第二个问题是,x是实数集,有正有负。为什么到了三角函数的n,教材中只取正整数?负的为什么不要了?
原因很简单,依然是正交。假设我们取了负数,有

可见,除了把系数弄的复杂化,没有任何好处!
3 三角级数的数学意义这个是形而上,需要重点把握的。
从线性代数的角度看,三角级数的本质是空间变换,将原本x空间的函数映射到三角函数空间。但不同于普通意义的线性代数,这里变换的是函数,而不是一般的实数。
这是学习FT最重要的一点。FT的数学意义必须在线性代数的角度理解。但微积分受限于学科,往往教材不会点明这点。至于信号与系统,压根不算数学书。然而线性代数的教材由于本身不涉及微积分,所以一般也不会说到FT。
细品上面的黑体文字!再给张图