我们都知道圆的周长、面积公式,球的表面积、体积公式,那么,你知道它们是怎么推导出来的。当然,仅仅凭借初中高中的数学是不可能推导出来的,我们初中高中只知道这个公式,而不知道所以然。
自从大学学了高等数学,学了牛顿和莱布尼茨发明的微积分,除了不定积分、定积分,还有二重积分,所以我们就能推导了。

圆的周长推导

圆的面积推导

球的表面积推导

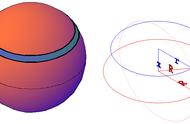
球的体积推导

圆

球
其实,球的表面积也可以用二重积分来推导,但是,用二重积分要用到二重积分、极坐标、偏导数等一系列知识,非常复杂,很难计算,所以不用这种方式来推导。这种方式推导球的表面积更简便快捷,且不用偏导数、二重积分,非常方便。
就这样,圆的面积和周长公式,球的表面积和体积公式就这么推导出来了。再拓展一下,椭圆的面积公式是S=πab,其中a是椭圆的长轴长度,b是椭圆的短轴长度,当b=a时,就是圆的面积公式,因为圆是椭圆的特殊情形(短轴等于长轴),可惜,椭圆没有周长,所以椭圆不可能有周长的。这和圆不一样。
有兴趣的朋友可以看看椭圆周长面积推导,就知道椭圆为什么没有周长。也可以看看用二重积分和偏导数求球的表面积。
其实,我想告诉大学生朋友们,高等数学其实不是头疼,难过的东西,如果吃进去了,懂得它的奥秘,它非常有趣。有好多东西值得探究。牛顿和莱布尼茨的微积分可以解决很多问题,很多东西。
好好学数学吧,学好数理化,走遍天下都不怕。
,