周朝时期,贵族往往具备六项技能,即礼、乐、射、御、书、数,后来孔子称之为“君子六艺”,因此早期文人骑马射箭计算等样样精通。南北朝时期,文人还没有像宋元明清时那样被扭曲,数学还没有被边缘化,是当时的“显学”之一。
作为南北朝时的大科学家,祖冲之可谓是家喻户晓,在数学、天文历法和机械制造上造诣惊人,尤其在圆周率探索上,首次将“圆周率”精算到小数第七位,即在3.1415926和3.1415927之间,直到16世纪时阿拉伯数学家阿尔·卡西才打破了这一纪录。
俗话说虎父无犬子,祖冲之之子有何成就呢?鲜为人知的是,祖冲之之子祖暅(gèng)在数学、天文上也有惊人的成就,其中有一项世界级成果,直到1100年后欧洲人才研究出来。让人惋惜的是,欧洲人研究出来之后,就以此人姓名命名研究成果,而祖暅却被世人遗忘。

两汉魏晋南北朝时,中国科学研究氛围还比较浓郁,汉朝建立了藏书楼石渠阁,南朝宋时设有朝廷研究机构华林学省,以及集藏书、研究和教学三位一体的机构——总明观。没有儒家的扭曲,在比较宽松的学术氛围刺激下,这一时期出现了不少著名科学家,比如东汉张衡、魏晋刘徽、南朝祖冲之与祖暅等。其中,祖冲之与祖暅的一些成就,与魏晋时的刘徽息息相关,而刘徽的成就之一就是在“圆”的计算上。
与西方不同,比如古希腊在没有急迫的现实需求以及丰富积累的情况下,突兀的出现了高超的几何学,而中国数学脉络比较明显,循序渐进从简单到复杂不断升级。首先,甲骨文上有九个单数以及“十、百、千”等数字,说明当时“十进制”已经出现。十进制是数学史上伟大发明,只需要九个数码就能表达一切数字,当时古希腊每个数字都要一个文字表示,罗马只有7个数码,玛雅是20进制需要19个数码,巴比伦是60进制需要59个数码,因此十进制的出现奠定了中国古代数学领先世界的基础。其次,在考古出土的秦简上有“九九乘法表”,史书上记载两汉魏晋筹算已能计算四则运算与开方。中国数学发展到这一步之后,对一些难题自然而然地产生了新的研究思路,比如在圆周率与球体积的问题上。

圆周率的应用很广泛,尤其是在天文、历法方面,凡牵涉到“圆”的一切问题,都要使用圆周率来推算。如何正确地推求圆周率的数值,是当时世界数学史上的一个重要课题。《周髀算经》和《九章算术》中就提出径一周三的古率,定圆周率为三,即圆周长是直径长的三倍。但囿于当时的数学知识,很难进一步深入研究,到了两汉魏晋时期,随着中国数学进一步发展,此时已经具备了深入研究的基础,比如东汉张衡推算出的圆周率值为3.162,三国时王蕃推算出的圆周率数值为3.155。
刘徽是魏晋大数学家,在中国最早明确主张用逻辑推理的方式来论证数学命题,著有《九章算术注》和《海岛算经》,他在数学上贡献很多,其中之一叫“割圆术”计算圆周率。《九章算术注》中记载“割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”,就是不断倍增圆内接正多边形的边数求出圆周率的方法,算得圆周率为3.14或157/50。割圆术不仅仅只是开创探索圆周率的精确方法,以及计算圆周率这么简单,更是人类历史上首次将极限和无穷小分割引入数学证明,具有非同一般的意义。
南北朝时期,祖冲之在刘徽的基础上,进一步研究了圆周率问题,将之精确到3.1415926和3.1415927之间,达到了当时数学知识能研究出的极限值。

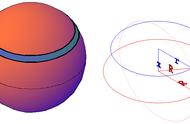
得出比较精确的圆周率之后,祖冲之开始研究球体积的计算问题,不过祖冲之并未解开,最终将毕生研究写成《缀术》一书。
祖冲之去世之后,祖暅一边继续从事数学、天文的研究,一边修补编辑《缀术》。在这一过程中,祖暅有了两项世界级发现。
首先,在研究球体积的过程中,他开创性地提出“缘幂势既同,则积不容异”,即夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等,这就是著名的祖暅公理。
其次,祖冲之与祖暅发现《九章算术》中的球体积计算公式是错误的,刘徽的“牟合方盖”理论也不正确,最终祖暅根据自己发现的“祖暅公理”,提出了“开立圆术”,巧妙地得到球体积的正确公式,解决了刘徽尚未解决的球体积问题。后来,祖暅将之补充到了《缀术》中,可惜这本书已经失传。
当然,尽管《缀术》失传了,但朝鲜与日本的古代文献中都提到过这本书,而且古代其他文献中也提到过,并摘取了包括祖暅公理、开立圆术在内的书中部分内容,比如唐代李淳风注《九章算术》时就提到开立圆术。

1635年,意大利数学家卡瓦列里在《连续不可分几何》一文中,提出了等积原理,但没有严谨的证明过程,实际上结论就是祖暅原理。尽管祖暅原理早了卡瓦列里1100多年,但如今国外称之为“卡瓦列里原理”,国内只有部分书籍中称之为“祖暅原理”。
明朝晚期,众多欧洲传教士来华,他们带来的只是一些零星的欧洲知识,却将大量中文书籍翻译并传播到西方,因此卡瓦列里究竟是独立研究出来的,还是参照了“祖暅原理”,还真是一个值得深思的话题。晚明中西方交流之前,欧洲在数学领域并没有什么惊人的发现,但在之后惊人的成果却层出不穷,或许这种现象已经说明了一切。
,