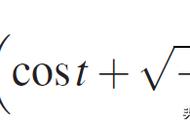这种问题经常在网络上出现,很容易让人陷入某种误区,甚至让人患上“强迫症”,看到无理数就会产生某种说不清道不明的“歧视”心理,就好像无理数真的“无理”一样,“无理数”这三个字确实蒙蔽了很多人的双眼!
事实上无理数一点也不“无理”,无理数和有理数完全是平等的,都是一个再普通不过的数,而且是真实存在的数,一个非常确定的数。

无理数与有理数的区别只有一点:无限不循环,仅此而已。
但你不能因为无限不循环就对无理数“另眼看待”,甚至会下意识地认为“无限不循环就不是确定的数”!
不少人总是下意识习惯性地强迫无理数必须用小数完全写出来,写不出来心里就憋得慌。但一个非常现实的问题是:为何一定要用小数写出来呢?用其他形式写出来不行吗?
这就是不少人认识山的误区!

比如说圆周率π就是π,就好比“1就是1”一样,都是一个确定的数。我可以很轻松地把π写出来,它就是:π。
明白了这点,再回到问题中。
1/3等于0.333......,永远写不完,但写不完不代表1/3就不存在,事实上你可以非常轻松地在数周上画出1/3长度,不但如此,你可以在数周上画出任何一个数(包括无理数)的长度,比如说π,√2等。

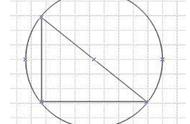
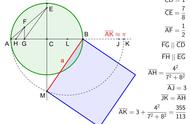
下图一眼就能看出如何在数轴上画出√2:画一个直角边为1的等腰直角三角形,然后以斜边为半径画一个圆形,与数轴的交点就是√2。