2、应用
分割法其实体现了一种很精妙的数学思想,那就是微分思想,我们对曲线进行不断的分割,份数越来越多,每一份也就越来越短,我么您就可以把极小的一段看成是直线了。这种思想在物理中的应用非常广泛,在高中物理学习匀变速直线运动的位移的时候,还需要利用这种思想,把时间分成无数段,那么每一极小段时间内(Δt趋近与零)就可以看成是匀速运动了,然后再通过积分思想来求匀变速直线运动的位移。

1、测量一段曲线的长度
步骤:
(1)测出硬币的圆周长C
(2)用硬币紧贴曲线,从一段滚到另一端,记下滚动的圈数n
(3)算出曲线长为L=nC

2、应用
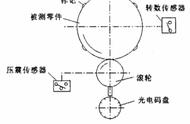
很多人可能觉得这个可操作性不强,实际上确实如此,我们很难保证曲线的长度刚好是周长的整数倍。但是这种方法在生活中应用却非常广泛,我们平时汽车和电动车仪表盘上都会先射里程数,就是根据滚轮法的原理计算出来的。汽车和电动车可以自动纪律轮胎转动的圈数,然后提前算出来轮胎的周长是多少,这样汽车和电动车就可以自动为我们计算我们开一次车到底跑了多远了。

1、测量一枚硬币的直径
步骤:
(1)使直角三角板的一条直角边与刻度尺左边的一段重合,调整三角板的位置使另一条直角边对准刻度尺上的某一条刻度线
(2)将硬币立放在刻度尺上,使其与三角边和直尺相切
(3)在硬币右端再放一个直角三角板,使其一条直角边与刻度尺右端重合,另一条直角边与圆周相切
(4)从刻度尺上读出两个直角三角板相互平行的两条直角边间的距离即为硬币的直径