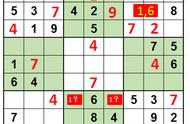
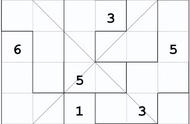
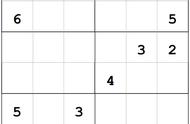
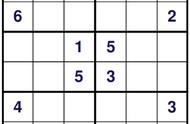
时至今日,数独(Sudoku)出现了越来越多的形态,比如《数独宇宙(Sudoku Universe)》中除了“标准数独”外,就包含有“*手数独”和“拼图数独”两种全新的数独题型,在玩法和规则上也是基于数独(Sudoku)的基础玩法并加以改进。
拼图数独,是在9x9的网格依然被划分为九部分,但每个部分不再是标准的3x3九宫格,而是九个相连方格组成的不规则区域。而你需要在每行每列以及每个不规则的区域内填入1~9的数字,不得重复。
而*手数独的独特之处在于,在标准数独的基础之上,还融合了数合游戏的玩法。数独网格中不再会预填数字作为提示,取而代之的是,网格被划分分多个虚线圈起来的区域,并给出区域内所有格子上数字的和作为提示。

当然,除此上述的三种玩法外,数独(Sudoku)还有着更多丰富的形态。比如:对角线数独、迷你数独、不规则数独、摩天楼数独、锯齿数独、连体数独等多种类型存在。甚至于还有更多的,被各地的数独爱好者们发明出的,全新的玩法和类型。
这些数独(Sudoku)的类型全部都是脱胎于“标准数独”,故而又被人们统称为——“变形数独”。

数独(Sudoku)的叫法起源于日本,其中“Sū”在日语中为数字的意思,“doku”则是单一的意思,合起来的意思是“在每一格只有一个数字”。
这也是现在数独(Sudoku)公认的英文名称。
但是,数独(Sudoku)的起源比叫法要早了很多。而被人们公认的数独(Sudoku)雏形,就是18世纪初瑞士数学家莱昂哈德·欧拉提出即n阶的方法——拉丁方阵。
拉丁方阵(英语:Latin square)是一种 n × n 的方阵,在这种 n × n 的方阵里,恰有 n 种不同的元素,每一种不同的元素在同一行或同一列里只出现一次。

19世纪80年代,一位美国的退休建筑师根据“拉丁方块”的原理,发明了一种趣味性极强的填字游戏。到了后来,这个游戏开始相继在美国的各大报纸上出现,当时的人们称呼这款游戏为“填数字(Number Place)”。
而这也是目前公认的数独(Sudoku)最早的见报版本。