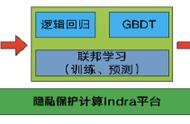
模型构建
传统统计学模型、机器学习模型和深度学习模型的构建方法各有不同,本文分别选择每个领域的经典模型,探索建模流程并比对各种构建方案的优缺点和适用性。
3.1、统计学模型ARMA建模流程
ARMA模型全名自回归滑动平均模型,是研究时间序列的重要方法,由自回归模型(简称AR模型)与移动平均模型(简称MA模型)为基础“混合”构成。它的基本思想是:某些时间序列是依赖于时间t的一组随机变量,构成该时间序列的单个序列值虽然具有不确定性,但整个序列的变化却有一定的规律性,可以用相应的数学模型近似描述。通过对该数学模型的分析研究,能够更本质地认识时间序列的结构与特征,达到最小方差意义下的最优预测,其具体建模流程如图4所示。

图4 ARMA模型建模流程图
由于ARMA模型是统计领域的模型,使用它必须首先满足序列平稳性这一前提条件。这是因为在大数定理和中心定理中要求样本同分布(这里同分布等价于时间序列中的平稳性),而统计领域的模型中有很多都是建立在大数定理和中心极限定理的前提条件下的,如果它不满足,得到的许多结论都是不可靠的。本文使用观察法和单位根法进行序列平稳检验。
观察法主要是通过序列自相关图和偏自相关图来观察序列的分布是否始终围绕一个常数上下浮动。单位根法是指通过单位根检验来检查序列中是否存在单位根,如果存在单位根就是非平稳时间序列了。单位根检验的原假设是存在单位根,因此如果得到的统计量显著小于3个置信度(1%,5%,10%)的临界统计值时,说明是拒绝原假设的。另外需要观察P-value是否非常接近0(4位小数基本即可)。


平稳序列