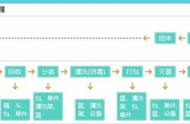
答案:
- 明确函数功能:jump(m, n)为跳到(m, n)位置。
- 寻找递归出口:不在边界之内 或 已走过。
- 明确所有路径:8个方位,技巧:这里可以用一个数组存入八个方位的变化,再用循环依次取出,比写八个方位要聪明许多。
- 回溯还原现场:path--; // 回溯法关键步骤a[m][n] = 0;
//马走日
class Sy2 {
private static int[][] next = { { 1, 2 }, { 1, -2 }, { -1, 2 }, { -1, -2 }, { 2, 1 }, { 2, -1 }, { -2, 1 }, { -2, -1 } }; // 马的跳跃路径(技巧)
private static int[][] map; // 地图
private static int m, n;
private static int count = 0;// 统计有多少种走法
private static int step = 0;
public static void main(String[] args) {
m = 5;
n = 5;
int x = 0;
int y = 0;
map = new int[m][n];
jump(x, y);
System.out.println("---------");
System.out.println(count);
}
private static void jump(int x, int y) {
// 如果超出界限,那就继续下一轮
if (x < 0 || x >= m || y < 0 || y >= n || map[x][y] != 0) {
return;
}
// 立足此节点
step ;
map[x][y] = step;
if (step == m * n) {
if (count == 0) // 如果是第一次,那就输出一个
show(map);
count ;
}
// 写出所有路径(技巧)
int tx = 0, ty = 0;
for (int i = 0; i < 8; i ) {
tx = x next[i][0]; // 技巧
ty = y next[i][1];
jump(tx, ty);
}
// 还原
step--;
map[x][y] = 0;
}
// 显示数组
private static void show(int[][] arr) {
for (int i = 0; i < m; i ) {
for (int j = 0; j < n; j ) {
System.out.print(arr[i][j] " \t");
}
System.out.println();
}
}
}
程序运行结果:

八皇后
编程解决“八皇后问题”:即 在一个 8*8 的矩形格子中排放 8 个皇后。
要满足的条件包括:任意两个皇后不能在同一行,同一列,也不能在同一条对角线上。
要求编程给出解的个数。
答案:
算法原理:回溯法
首先,可归纳问题的条件为,8 皇后之间需满足:
- 不在同一行上
- 不在同一列上
- 不在同一斜线上
- 不在同一反斜线上

这为我们提供一种遍历的思路,我们可以 逐行 或者 逐列 来进行可行摆放方案的遍历,每一行(列)遍历出一个符合条件的位置,接着就到下一行(列)遍历下一个棋子的合适位置,这种遍历思路可以保证我们遍历过程中有一个条件是绝对符合的——就是下一个棋子的摆放位置与前面的棋子 不在同一行 (列)。
这里我们 逐列摆放 , 数组下标代表列号,用数组元素存放行号。
把当前列 N 的前面的某一列设为 m,则 m 的所有取值为{m>=0,m<N}的集合,故又可在上面式子的基础,归纳为如下:

从这个图可以看出, m和N若在同一斜线上 ,那么 行差Am 和 列差AN 应该 相等 。