浙江华图 杨弋
数学运算在整个行测中占据了很重要的位置,15道题目,并且难度较大,所以总分值能达到15分以上,我就自己在教学过程中的心得体会与大家分享。在数学运算的一些常考题型中,很多必考的题型我们都能知道,比如说排列组合,工程问题,经济利润和容斥原理等,这些问题我们都能预测到,并且在教学的过程中都反复强调其重要性,反复在让学生练习,但是最后考试的情况并不尽如人意,究其原因是在于这些题型变化灵活,我们老师在上课中也没能很好得总结,考生没有彻底掌握,所以导致失分。在我看来,容斥原理这种题型每年是必考的,并且该题型固定,方法也较有针对性,我似乎也对这种题型情有独钟,在上课中我也会更加的仔细认证,所以我觉得上过培训班的学生一定能很好的掌握容斥原理这种题型与解法,并在考试中遇到此类问题能胸有成竹。
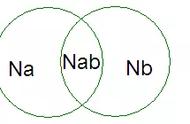
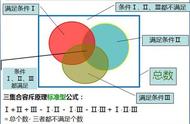
容斥原理在上课的过程中,我一般分为5块内容讲,即对应于5种不同的题型。第一种是两集合标准型的容斥原理,这类问题由简单的例子导出公式,满足条件1 满足条件2-两者都满足=总数-两者都不满足。第二种就是三集合标准型的容斥原理,三个硬币叠成两两有交集的图形,最后求这个图形的面积以此推导出三集合标准型的公式,强调只有当题目的条件和提问都能完全符合公式时我们才能用公式求解。作为引入第三种题型,在讲义上可以放一道不能完全代入三集合标准型公式求解的题目,比如题目出现求只满足两项的,可以推导出第3种题型,A B C-只满足2项的-2三项都满足的=总数-三项都不满足的。其实还可以导入第4种方法,即只满足1项 只满足2项 三项都满足=总数。再根据人数与人次之间的转化,可以建立另一个方程来求解。这四种方法是层层引入的,在教学中要注意循序渐进。最后为保证学员能得分,可以再介绍图示法,告知所有的容斥原理都可以用图示法解决,在忘公式或不能完全代公式的时候,这种方法就尤其好用,在运用时要注意标数一定是从里往外标,并注意“只”和“都”的区别,如果这5种方法都能学好,我相信遇到此类问题应该不会惊慌。
以上是我对运算中容斥原理的上课心得与体会,同时我还相信,作为老师应该从学生的角度出发,为学生能在考试中得高分一直是我们奋斗的目标。所以我觉得熟能生巧,不管什么科目什么题型,只要我们能下苦工,能去深层次得挖掘并能帮学生总结出考点和不同的题型方法,就一定能让考生满意,能让学生在考试中发挥出水平。
,