北京市第二届迎春杯数学竞赛决赛试题:
1到200的自然数中,即不是3的倍数,也不是5的倍数的数有多少个?如果把它们排成一列,第93个数是几?

可先求出3的倍数的个数:66个,5的倍数的个数:40个。既是3的位数也是5的倍数,即15的倍数的个数:13个。
然后,运用容斥原理,计算出结果:107个。

容斥原理是奥数四大原理之一,掌握它对于以后集合论的学习有很大的帮助。
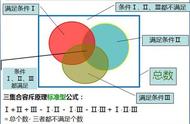
在解决计数问题时,必须做到不重复,不遗漏。为了使重叠部分不被重复计算,人们研究出一种方法,基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果 既无遗漏又无重复,这种计数的方法称为容斥原理。
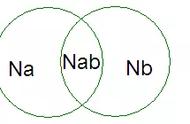
下图运用韦恩图,帮助你理解本题中的容斥原理:

第二问,求第93个数是几,可以倒着数回去,93个数即倒数15个数:

因此,第93个数是173。
如果想看完整视频讲解,请关注头条号:王老师讲奥数。
,