例题导入
某次考试有两道题目,答对第一题有24人,答对第二题的有16人。两题都答对的有9人,两题都答错的有4人。问:总共有多少人参加考试?

先上答案:共有35人参加考试。这是一道容斥问题,可以让孩子通过画文氏图,来理清不同部分之间关系,我是王老师,专注于小学数学!初步接触建议先从文氏图的概念入手,今天带同学们重点认识下文氏图。
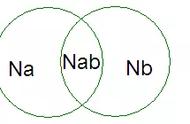
文氏图(Venn图)我们根据这次考试答题情况对同学进行分类,用不同颜色圆圈表示不同分类。
这就是文氏图。

① 答对第一题的有24人,我们用红线圆圈把他们圈起来;
② 答对第二题的有16人,我们用蓝线圆圈把他们圈起来;
③ 两道题都答对了的有9人,它们在图中哪里呢?
没错,就是两个圆的重叠部分,用黄色区域表示。
④ 两道题都没答对的有4人,我们用方框表示全部的同学,它们就在圆圈外面了。
解题步骤图画好了,开始解题了!
思路一
我们通过图来观察:

① 只答对第一题的同学有:24-9=15人
② 只答对第二题的同学有:16-9=7人
③ 两道全对有9人,全错的4人。
四部分相加正好是全部参加考试人数
所以参加考试人数:15 7 9 4=35人。
思路二
① 先分析至少一题做对的同学有多少人。
(24 16) 吗?发现重叠部分被多算了一次。
→ 24 16-9=31人。
② 参加考试的还有两道题都答错的4人
→ 31 4=35人。
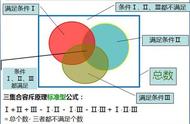
容斥原理通过上面例子,家长可以顺便介绍下容斥原理的知识了。
容斥原理,是一种计数方法。"容"表示包含;"斥"表示排除。意思是先把各种情况都"包含"进来,加在一起;再"排除"重复的部分,减去重复数。
举一反三你学会画文氏图了吗?做道练习题试下吧!欢迎评论区留下您的答案。
五一班学生参加语文兴趣小组的有28人;参见数学兴趣小组的有29人;12人两个小组都参加了。还有5个人两个小组都没参加,请问五一班一共多少人?

欢迎关注王老师头条号及数学专栏
学习更多好玩有趣的数学干货知识
,