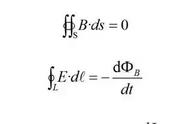电容公式推导口诀,电容计算公式口诀

设，V0 为电容上的初始电压值；V1 为电容最终可充到或放到的电压值；Vt 为t时刻电容上的电压值。则:

Vt=V0 （V1-V0）× [1-exp(-t/RC)]

t = RC × Ln[(V1 - V0)/(V1 - Vt)]

例如，电压为E的电池通过R向初值为0的电容C充电 , V0=0，V1=E，故充到t时刻电容上的电压为：

Vt=E × [1-exp(-t/RC)]

再如，初始电压为E的电容C通过R放电 , V0=E，V1=0，故放到t时刻电容上的电压为：

Vt=E × exp(-t/RC)

又如，初值为1/3Vcc的电容C通过R充电，充电终值为Vcc，问充到2/3Vcc需要的时间是多少？

V0=Vcc/3，V1=Vcc,Vt=2*Vcc/3，故

t=RC × Ln[(1-1/3)/(1-2/3)]=RC × Ln2 =0.693RC

注：以上exp()表示以e为底的指数函数；Ln()是e为底的对数函数

RC回路充放电时间的推导过程需要用高等数学，简单的方法只要记住RC回路的时间常数τ=R×C，在充电时，每过一个τ的时间，电容器上电压就上升（1-1/e）约等于0.632倍的电源电压与电容器电压之差；放电时相反。如C=10μF，R=10k，则τ=10e-6×10e3=0.1s 在初始状态Uc=0时，接通电源，则过0.1s（1τ）时，电容器上电压Uc为0 （1-0）×0.632=0.632倍电源电压U，到0.2s（2τ）时，Uc为0.632 （1-0.632）×0.632=0.865倍U……以此类推，直到t=∞时，Uc=U。放电时同样运用，只是初始状态不同，初始状态Uc=U。

进入正题前，我们先来回顾下电容的充放电时间计算公式，假设有电源Vu通过电阻R给电容C充电，V0为电容上的初始电压值，Vu为电容充满电后的电压值，Vt为任意时刻t时电容上的电压值，那么便可以得到如下的计算公式：

Vt = V0 (Vu – V0) * [1 – exp( -t/RC)]

如果电容上的初始电压为0，则公式可以简化为：

Vt = Vu * [1 – exp( -t/RC)]

由上述公式可知，因为指数值只可能无限接近于0，但永远不会等于0，所以电容电量要完全充满，需要无穷大的时间。

当t = RC时，Vt = 0.63Vu；

当t = 2RC时，Vt = 0.86Vu；

当t = 3RC时，Vt = 0.95Vu；

当t = 4RC时，Vt = 0.98Vu；

当t = 5RC时，Vt = 0.99Vu；

可见，经过3~5个RC后，充电过程基本结束。

当电容充满电后，将电源Vu短路，电容C会通过R放电，则任意时刻t，电容上的电压为：

Vt = Vu * exp( -t/RC)

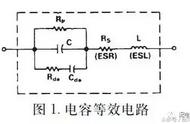
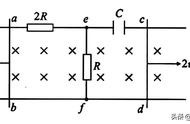
对于简单的串联电路，时间常数就等于电阻R和电容C的乘积，但是，在实际电路中，时间常数RC并不那么容易算，例如下图(a)。

对于上图(a)，如果从充电的角度去计算时间常数会比较难，我们不妨换个角度来思考，我们知道，时间常数只与电阻和电容有关，而与电源无关，对于简单的由一个电阻R和一个电容C串联的电路来说，其充电和放电的时间参数是一样的，都是RC，所以，我们可以把上图中的电源短路，使电容C1放电，如上图(b)所示，很容易得到其时间常数：

t = RC = (R1//R2)*C

使用同样的方法，可以将下图(a)电路等效成(b)的放电电路形式，得到电路的时间常数：

t = RC = R1*(C1 C2)

用同样的方法，可以将下图(a)电路等效成(b)的放电电路形式，得到电路的时间常数：

t = RC = ((R1//R3//R4) R2)*C1

1).如果RC电路中的电源是电压源形式，先把电源“短路”而保留其串联内阻；

2).把去掉电源后的电路简化成一个等效电阻R和等效电容C串联的RC放电回路，等效电阻R和等效电容C的乘积就是电路的时间常数；

3).如果电路使用的是电流源形式，应把电流源开路而保留它的并联内阻，再按简化电路的方法求出时间常数；

4).计算时间常数应注意各个参数的单位，当电阻的单位是“欧姆”，电容的单位是“法拉”时，乘得的时间常数单位才是“秒”。

对于在高频工作下的RC电路，由于寄生参数的影响，很难根据电路中各元器件的标称值来计算出时间常数RC，这时，我们可以根据电容的充放电特性来通过曲线方法计算，前面已经介绍过了，电容充电时，经过一个时间常数RC时，电容上的电压等于充电电源电压的0.63倍，放电时，经过一个时间常数RC时，电容上的电压下降到电源电压的0.37倍。

如上图所示，如通过实验的方法绘出电容的充放电曲线，在起点处做一条充放电切线，则切线与横轴的交点就是时间常数RC。