椭圆形平面图形的建筑物具有平面布局较为紧凑、并且富有动态感等优点,多用于公共建筑,尤其在体育性建筑中使用较多。比如,在椭圆形的体育馆中,观众席能获得良好的视觉质量,各个方位的席位都具有良好的清晰度。
椭圆形平面曲线的数学方程式
根据数学定义可知:平面内到两定点F1、F2的距离之和等于常数的点的轨迹叫做椭圆。两个定点F1、F2叫做椭圆的焦点,两焦点间的距离叫做焦距, 焦距等于2C, 即F1F2=2C(c>0)。
如图所示,设点M(x、y)是椭圆上任意一点,则MF1与MF2,两段距离之和为一定值设为2a,即MF1 MF2=2a(a>0)
在三角形MF1F2中,MF1 MF2>F1F2,(三角形两边之和大于第三边),即2a>2c,a>c,取过焦点F1,F2的直线为x轴,线段F1,F2的垂直平分线为y轴,建立直角坐标系,设椭圆上任一点M点的坐标为(x,y),MF1与MF2的距离,根据勾股定理,用坐标值来表示:
(MF1)^2=(x c)^2 y^2,(MF2)^2=(x-c)^2 y^2,
根据椭圆定义: MF1 MF2=2a
因为a>c,可设b^2=a^2-c^2
则上述方程式为: x^2/a^2 y^2/b^2=1,就可得到椭圆的标准方程式:
这个方程式所表示的椭圆的焦点在x轴上,焦点坐标为F1(-C,0)、F(c,0),这里c²=a²-b²。椭圆对称于x轴,在x轴方向称为长轴,其值为2a,在y轴方向称为短轴,其值为2b,与x、y轴的交点A1、A2、B1,B2称为椭圆的四个顶点。
如果椭圆的焦点在y轴上,如图2-7所示,只要将上面方程式中的x、y互换后就可得到它的标准方程式:
y^2/a^2 x^2/b^2=1
在椭圆方程式中,当a、b值一定时,只要知道变量x和其中一个数值,便可求得椭圆曲线上的任何一个数值,即
y=±b/a* a²-x²
或x=±a/b*(b²-x²)½
椭圆形平面曲线的作图方法
椭圆形平面曲线的作图方法,常用的有以下几种。
一、同心圆法
当已知椭圆的长轴(2a)和短轴(2b)的尺寸后,可用同心圆法求作其椭圆曲线。
作图步骤:
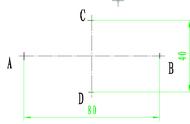
1.作椭圆的长轴AB和短轴CD,如图
2.如图所示:
(1)分别以AB和CD为直径作大小两同心圆。
(2)等分两同心圆为若干份,例如十二等分。
3.如图所示:
(1)从大圆各等分点作竖向直线,与过小圆各对应等分点作的水平线相交,得椭圆曲线的各点。
(2)将其各点顺滑连接起来,即为所求作的椭圆曲线。

同心圆作椭圆
二、四心圆法
当已知椭圆的长轴(2a)和短轴(2b)的尺寸后,可用四心圆法求作其近似的椭圆曲线。作图步骤:
1.作椭圆的长轴AB和短轴CD
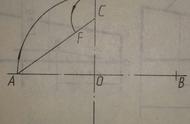
2.如图所示:
(1)连接AC。
(2)以0为圆心,OA为半径作圆弧,交CD延长线于E点。
(3)以C为圆心,CE为半径作圆弧,交AC于F点。
(4)作AF的垂直平分线,交长轴于O1,交短轴〈或其延长线)于O2。
(5)在OB轴上截取OO₃=OO₁,在OC轴上截取OO4= OO2
3.如图:
(1)分别以O₁、O2、O₃、O4为圆心,以O₁ A、O2C、O₃B、O4D为半径作圆弧。
(2)使各弧段在O2O₁, O2 O₃和O4 O₁, O4 O₃的延长线上的G、I、H、J四点处相交,则所得的封闭曲线即为所要求作的近似的椭圆曲线。

四心圆作椭圆
椭圆形平面曲线的施工放线
椭圆形平面曲线的现场施工放线,其方法也是很多的,常用的方法有直接拉线法(即连续运动法),几何作图法和坐标计算法等,现将有关放线方法分述如下。
一、直接拉线法
这种放线方法在椭圆形平面尺寸较小时常采用,这种放线方法操作比较简单,放线速度快,只要操作认真,可以获得一定的精确度。
某纪念碑建筑的外围围墙形状为一椭圆形,椭圆长轴的设计尺寸α=15m,短轴的设计尺寸b=9m。试用直接拉线法进行现场施工放线。
(一)放线步骤
1.根据总平面设计图,确定纪念碑平面图形中心点位置和主轴线(即椭圆的短轴)方向,并正确放出长轴位置。
2.根据已知的长、短轴设计参数a=15m,6=9m,定出椭圆形平面的四个顶点位置,即A(-15,0)、B(15,0)、C(0,9)、D(0,-9)。并计算出椭圆的焦距和确定焦点位置。焦距c=12m
3.在焦点F1和F2处建立较为稳固的木桩或水泥桩。
4.找细铁丝一根,其长度等于F1c F2c(等于2a),两端固定于F1,F2上,然后用圆的铁棍或木棍套住细铁丝后在长轴两边画曲线,即可得到一条符合设计要求的椭圆形曲线,如图2-16所示。
(二)用直接拉线法作椭圆形平面曲线的现场施工放线,应注意以下问题:
1.两焦点上设置的桩,位置应正确,设置应稳固,施工中应妥善保护。
2.所用拉线材料不应有伸缩性,描画曲线过程中,应始终拉紧,不应有时紧时松的现象。
三、坐标计算法
当椭圆形平面曲线的尺寸较大,或是不能采用直接拉线法进行施工放线时,常采用坐标计算法进行现场施工放线。计算方法和圆弧曲线的坐标计算法相同。通过坐标计算,最后列成表格,供现场放线人员使用,施工操作较简单,能获得较好的精度。
某纪念碑建筑的外围围墙形状为一椭圆形,椭圆长轴的设计尺寸a=15m,短轴的设计尺寸b=9m。试采用坐标计算法进行椭圆形平面的施工放线。
(一)坐标计算
1.根据已知条件,椭圆长轴的设计尺寸a=15m,短轴设计尺寸b=9m,列出该椭圆的标准方程式x^2/15^2 y^2/9^2=1
2.把方程式变为y=±9/15(15^2-x^2)½
3.将x=0、1、2……15各点代入方程式,求出相应的y值,最后将计算结果列成表格,注:y值均为正负对称值。
(二)施工放线
1.根据总平面设计,确定纪念碑椭圆形平面的中心点位置和主轴线(短轴)方位。
2.以主轴线为y轴,以中心点为原点,建立直角坐标,x轴即为椭圆形平面的长轴线。
3.在×轴上分别取x=1、2、3......15各点,并通过上述各点作垂直线,根据表2-2所列数值,分别量取各点y值,y0=±9;y1=±8.98;y2=±7.92......y15=0,
4.根据椭圆曲线的对称原理,可确定左侧半边,即x=0-15范围的各点y值。
5.将各点比较顺滑的连接起来,即可得到一条符合设计要求的椭圆曲线(即围墙中心线)。
当x轴上取的点数越多,所求作的椭圆曲线也越顺滑,越精确。

椭圆形建筑
,