本文为“第三届数学文化征文比赛
温故建构新知 论证生成巧思
——三角形的中位线定理的探究
作者: 王玉娇 郑 林
作品编号:020
【摘要】本文借助平行四边形的对角线互相平分是三角形中位线定理的最近知识生长点,引出概念并建构模型探讨不同视角下的论证方法。进而通过古题新做打破固有思维、完成知识的吸收和内化。本文旨在提升学生的探究水平和知识的迁移能力。
现行人教版教材涉及三角形中位线定理的概念教学中缺少且内容衔接不够自然。
【关键词】中位线;平行四边形;定理;论证;
数学是研究空间模型和数量关系的一门系统学科。而三角形的中位线既体现了线段的数量关系又体现了位置关系,本节课是数学之美的体现,也是承上启下衔接各知识点间的桥梁。本文主要从三角形中位线定理概念的生成、定理的论证及知识的巩固三个部分进行探究。现行人教版的初中数学把三角形的中位线定理放在18.1.2平行四边形的判定(2)中来学习,体现了需要利用平行四边形的知识来探究三角形中位线定理的设计意图。但是教材和大部分教师在引入或者概念的生成部分的设计与平行四边形是独立的,内容衔接上不够自然,且缺少探索发现该定理的过程。事实上三角形和平行四边形是相互关联的,这样直接切入显得生硬和知识的断层。本文的创新之处在于,直接利用平行四边形的一道习题变式作为引入,利用平行四边形的性质顺势发现、提出、论证三角形的中位线定理,前后衔接过渡更加自然,而不必另辟蹊径,创设更多陌生情境[1]。
一、类比联想获新知:概念的生成过程
在三角形中位线定理的教学中,基于无法迅速优化教材,那身为教师可以选取一种策略作为教材与学生之间的衔接桥梁。在根据平行四边形性质的关联性增设中位线定理的发现过程中,激发学生的潜能和学习数学的兴趣。激发学生的学习兴趣不在于片面的追求新和怪,如果能从学生熟悉的原教材、旧例题中挖掘出具有启发性的东西更能激发学生的求知欲。本环节立足于学生已有的认知,在此基础上达到最近的发展区水平,这样的教学设计更能激发学生独自钻研的主动性和发现数学知识间的环环相扣之美。
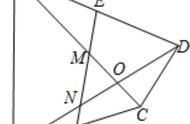
例题引入:如图1,平行四边形ABCD的对角线AC,BD相交于点O,
(1)点O平分哪些线段?
(2)如图2,当线段BD所在的直线绕点O旋转,分别交线段AB,CD于点E、F,点O平分线段EF吗?

(3)如图3,在旋转过程中,当点E为线段AB的中点时,我们可以得到那些特殊的结论?
结论:点F为线段CD的中点;从位置关系看EF//BC;从数量角度看。
(4)去掉图3中平行四边形ABCD的对角线AC右侧部分的图形,得到如图4所示的三角形,则EO是连接△ABC的两边AB,AC中点的线段。像EO这样,连接三角形两边中点的线段叫做三角形中位线[2]。

(5)探究:三角形的中位线有什么性质?
从(3)中归纳得到定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半[2]。
设计分析:本例题是平行四边形的性质课时的经典拓展题,上节课学生通过平行四边形的性质易证无论EF所在直线绕O点如何旋转总有△AOE≌△COF,本节课继续探究当EF所在直线旋转成如图3所在的特殊位置时能自然得出三角形的中位线定理。本例题不但实现了课时上和知识点上的衔接,而且实现了平行四边形和三角形间的互相转化,为后面定理的论证提供了辅助线的添加思路。同时让我们明白对“旧”知识与“旧”例题的深入挖掘往往会有意想不到的惊喜。
二、探索碰撞生巧思:定理的论证过程
如何让知识在思维里生长?学生只有在自我探索、实践中不断建构、优化、类比才能深刻体会三角形与平行四边形间的相互转化关系。我们借助三角形中位线定理的论证过程来继续深化认知。本环节可以遵循分析思路——添加辅助线——进行论证三步原则进行。借助引课的例题分析从不同视角得出不同的论证方法。
(一) 论证视角:建构平行四边形
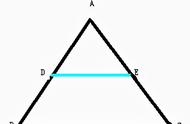
如图5,在△ABC中,D,E分别是AB,AC的中点,连接DE。求证:DE∥BC,且 。

方法一:(倍长中线模型1)如图6,延长DE至点F,使EF=DE,联结CF,可证△ADE≌△CFE,得到平行四边形DBCF,因此得出DE∥BC,且。