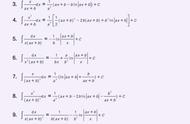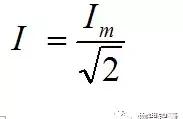对于积分,首先要有微元法的思想,先简单地引入定积分定义来源:分割-做乘积-求和-取极限。而微元法思想,一直贯穿考研数学的核心,即使到后面的概率论中求概率密度和分布函数,依然需要用微元法的思想。万物皆可微。
对于变换“元”的方法有哪些呢?
时间“元”与空间“元”,点元-线元-面元-体元,均匀-非均匀,直线-曲线。对于极坐标系还有角“元”和弧“元”等等。
根据题目明确对何种元素进行分割?是把曲线分割成很多个一小段,还是把块切成很多个一小薄片?先把分割后某一点处的微元表示出来,然后积分区域累加,最后选用合适方法计算所表示出来的积分。
第一型第二型曲线积分依然要运用微元法的思想。
1.对于第一型曲线积分,其物理意义是求曲线杆的质量,几何意义是对弧长的曲线积分。

定义和性质如下:

基本计算方法:直接法、利用奇偶性、利用对称性、利用形心坐标

对于(1),ds=根号下(dx dy),提出一个dt到根号外,同时在根号内同除dt,就可得到(1)式。
对于(2)是把x看成参数:y=y(x),x=x。ds=根号下(dx dy),提出一个dx到根号外,同时在根号内同除dx,就可得到(2)式。
对于(3)把θ看成参数。