最近看到金太阳的一道题目,难度不大,分享如下:

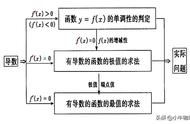
题目用基础的指对数放缩即可,若用凸凹反转,此时如何分组,若参考上题考虑右侧,能否分组成证明xe^x-x²-2>2lnx-x?只看左侧,因为xe^x比e^x的增长速率更快,而指数函数在增长又快于幂函数,因此左侧函数能大致判断出单增,不存在极小值点。
题目分组有两种方法,因为e^x/x为常见指数模型,不等式两侧同除x²,如下:

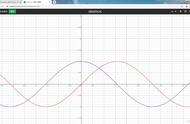
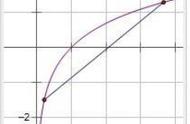
除了两端点的极限之外,又因为x=1时右侧函数为1,因此右侧函数的趋势可能为先增后减,存在极大值点,左右图像为:


最近看到金太阳的一道题目,难度不大,分享如下:

题目用基础的指对数放缩即可,若用凸凹反转,此时如何分组,若参考上题考虑右侧,能否分组成证明xe^x-x²-2>2lnx-x?只看左侧,因为xe^x比e^x的增长速率更快,而指数函数在增长又快于幂函数,因此左侧函数能大致判断出单增,不存在极小值点。
题目分组有两种方法,因为e^x/x为常见指数模型,不等式两侧同除x²,如下:

除了两端点的极限之外,又因为x=1时右侧函数为1,因此右侧函数的趋势可能为先增后减,存在极大值点,左右图像为:













Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.