一、利用导数求瞬时值
某物理量A定义为A=△y/△x,
比如:速度v=△x/△t,加速度a=△v/△t,角速度ω=△θ/△t,电场强度E=-△Φ/△x,感应电动势E=N△Φ/△t等等,凡是结构是A=△y/△x这种类型的,我们都可以采用类比的方法.
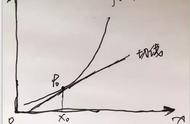
物理量A=△y/△x,若△x不趋近零时,是一个过程的平均值,反映在图像上就是割线斜率;
物理量A=△y/△x,若△x→0,A的值为某时刻或某点的瞬时值,也就是△x→0的极限,

反映在图像上就是切线的斜率.

①导数在运动学上的运用
示例1:某质点运动过程中位移x(单位m)和时间t(单位s)满足表达式,x=5t³ 3t² 4t 2(m),求:
①1s—3s内的平均速度
②2s时的瞬时速度
③2s时的加速度
【解析】
①1s—3s内的平均速度是割线斜率,
t=1s时,x=14m;
t=3s时,x=176m;
△x=162m;
1s—3s内的平均速度为81m/s.
②2s时的瞬时速度是切线斜率,瞬时速度的表达式就是位移对时间的导数,求得:
v=15t² 6t 4(m/s)
当t=2s时,v=76m/s.
③瞬时加速度的表达式就是速度对时间的导数,就是v-t图的斜率,也就是x-t函数对时间t的二阶导数.
求导得:a=30t 6(m/s²)
t=2s时,a=66m/s².
②导数在感应电动势上的运用
示例2:如图所示,两根平行足够长的金属导轨固定在水平桌面上,导轨的端点P和Q用导线相连,两导轨间的距离为L,磁场垂直于桌面向上,已知磁感强度B与时间的关系为B=kt(k为大于零的常量).在t=0时刻,金属杆紧靠在P、Q端,在外力作用下,杆从t=0时刻开始以恒定的加速度a从静止开始向导轨的另一端滑动,求在t时刻整个回路的感应电动势大小.