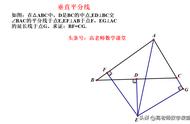
求证:∠B=∠CAF。
分析:∠B与∠CAF不在同一个三角形中,又∵∠B,∠CAF所在的两个三角形不全等,所以欲证∠B=∠CAF,不能利用等腰三角形或全等三角形的性质. 那么注意到EF垂直平分AD,可得FA=FD,因此∠FAD=∠ADF,又因为 ∠CAF=∠FAD-∠CAD,∠B=∠ADF-∠BAD,而∠CAD=∠BAD,所以可证明∠CAF=∠B.
证明:∵EF垂直平分AD(已知),
∴FA=FD(线段垂直平分线上的点和这条线段的两端点的距离相等).
∴∠FAD=∠ADF(等边对等角)
∵∠B=∠ADF-∠BAD(三角形的一个外角等于和它不相邻的两个内角的和),∠CAF=∠FAD-∠CAD,
又∠CAD=∠BAD(角平分线定义),
∴∠B=∠CAF .
说明:运用线段的垂直平分线的定理或逆定理,能使问题简化,如本例题中,EF垂直平分AD,可以直接有结论FA=FD,不必再去证明两个三角形全等.
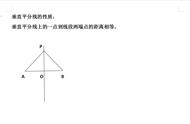
例4.如图,已知直线l和点A,点B,在直线l上求作一点P,使PA=PB.

分析:假设P点已经作出,则由PA=PB,那么根据“到线段两端点距离相等的点在这条线段的垂直平分线上”可知,点P在线段AB的垂直平分线上. 而点P又在直线l上,则点P应是AB的垂直平分线与垂线l的交点。
作法:1.连结AB.
2.作线段AB的垂直平分线,交直线l于点P.则P即为所求的点.
说明:在求作一个点时,要考虑该点具备什么样的特点,如它到一条线段的两个端点距离相等,它就在连结这两点的线段的垂直平分线上,如果它到一个角的两边的距离相等,它就在这个角的平分线上.
看完了垂直平分线的相关知识点和例题,我们来做一下有关于垂直平分线的练习题。


以上就是极客数学帮为大家整理的有关垂直平分线的全部内容了。
,