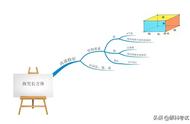
最大公因数和最小公倍数的知识应用:
1:一张长方形纸长24厘米,宽16厘米,如果要剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是多少厘米?可以剪几个正方形?
解题思路:正方形的边长一定是长和宽的公因数,且是最大公因数。

答:剪出的正方形的边长最大是8厘米。可以剪6个正方。
最大公因数的应用的关键词:“最大”、“最长”、“最多”等。
知识应用2:甲、乙两人去图书馆看书,甲每6天去一次,乙每8天去一次。如果4月1日他们两个在图书馆相遇,那么下一次在图书馆相遇是几月几日?
解题思路:他们两个下次在图书馆相遇所经过的天数一定是6和8的公倍数,且是最小公倍数。

答:他们下一次在图书馆相遇是4月25日。
知识应用3:一群学生去春游,去时12个人坐一辆车刚好,回来时8个人坐一辆车刚好。这群学生最少有多少人?
解题思路:12刚好8也刚好,那么总人数一定是8和12的公倍数,最少多少人就是求最小公倍数。
12=2×2×3 8=2×2×2 最小公倍数 2×2×3×2=24
答:这群学生最少有24人。
最小公倍数的应用的关键词:“最少”、“最小”、“至少”等。

第三单元 长方体和正方体
1、由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。长方体和正方体都是立体图形。正方体也叫立方体。
2、相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。(长、宽、高都各有4条,分别平行并且相等)
3、长方体的特征:
① 面:有6个面,都是长方形(特殊情况下最多有两个相对的面是正方形)。相对的面完全相同。
② 棱:有12条棱。相对的棱长度相等。
③ 顶点:有8个顶点。
4、正方体的特征:
① 面:有6个面都是正方形,6个面完全相同。
② 棱:有12条棱。12条棱的长度相等。
③ 顶点:有8个顶点。
相同点 | 不同点 | ||
面 | 棱 | ||
长方体 | 6个面, 12条棱, 8个顶点。 | 6个面都是长方形。(有可能有两个相对的面是正方形)。 | 相对的棱的长度都相等 |
正方体 | 6个面都是正方形。 | 12条棱都相等。 | |
5、正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
至少要8个小正方体才能拼成一个稍大的正方体。
经过折叠可以组合成长方体: