第三章:不等式(1)定理:如果a,b∈R,那么a2+b2≥2ab,当且仅当a=b时,等号成立.(2)定理(基本不等式):如果a,b>0,那么a+b2____ab,当且仅当______时,等号成立.也可以表述为:两个____的算术平均__________________它们的几何平均.(3)利用基本不等式求最值:对两个正实数x,y,①如果它们的和S是定值,则当且仅当______时,它们的积P取得最____值;②如果它们的积P是定值,则当且仅当______时,它们的和S取得最____值.2.三个正数的算术—几何平均不等式(1)定理如果a,b,c均为正数,那么a+b+c3____3abc,当且仅当________时,等号成立.即三个正数的算术平均________它们的几何平均.(2)基本不等式的推广对于n个正数a1,a2,...,an,它们的算术平均________它们的几何平均,即a1+a2+...+ann____na1a2...an,当且仅当______________时,等号成立.3.利用均值不等式求最值遵循的原则:“一正二定三等”(1)正:使用均值不等式所涉及的项必须为正数,如果有负数则考虑变形或使用其它方法(2)定:使用均值不等式求最值时,变形后的一侧不能还含有核心变量,例如:当0,x求23yxx的最小值。此时若直接使用均值不等式,则2324yxxx,右侧依然含有x,则无法找到最值。①求和的式子→乘积为定值。例如:上式中24yxx为了乘积消掉x,则要将3x拆为两个2x,则2223342222334yxxxxxxxx②乘积的式子→和为定值,例如302x,求32fxxx的最大值。则考虑变积为和后保证x能够消掉,所以2112329322322228xxfxxxxx(3)等:若能利用均值不等式求得最值,则要保证等号成立,要注意以下两点:①若求最值的过程中多次使用均值不等式,则均值不等式等号成立的条件必须能够同时成立(彼此不冲突)②若涉及的变量有初始范围要求,则使用均值不等式后要解出等号成立时变量的值,并验证是否符合初始范围。一、1的秒用命题特点分析:此类题目主要特点是:1、两个变量是正实数(使用基本不等式的前提),2、有一个代数式①的值已知,求另一个代数式②的最小值,其中两个代数式一个是整式axby,一个是分式mnxy,当然会在此基础上进行变形。解题方法荟萃:主要是凑出可以使用基本不等式的形式:yxxy的形式,多数情况下是让两个代数式相乘。例题1.(1)已知,xyR,21xy,求12xy的最小值;(2)已知,xyR,23xy,求12xy的最小值;(3)已知,xyR,322xy,求62xy的最小值;(4)已知,xyR,2xyxy,求2xy的最小值;【解析】这四个题目中,(1)是“1的替换”的最基础题目,已知整式的值为1,求分式的最小值,(2)是将已知值变成了3,需要调节系数,(3)是已知分式的值求整式的最值,(4)对分式进行等价变换。【答案】(1)121222(2)()145249xyxyxyxyyx当且仅当22xyyx即13xy时取等号(2)121121221(2)()145243333xyxyxyxyyx()()当且仅当22xyyx即13xy时取等号(3)1323662=()(62)9218622yxxyxyxyxy当且仅当63xyyx即32 222xy时取等(4)因为2xyxy,所以121yx,然后1242=( 2y)( )=48xyxyxyxyx当且仅当4xyyx即24xy时取等号例题2.(1)已知,xyR,1xy,求1213xy的最小值;(2)已知,xyR,1xy,求2211xyxy的最小值;(3)已知,xyR,1xy,求1223xyy的最小值;(4)已知,xyR,231xy,求123xyy的最小值;【解析】这四个题目是便是比较大的四个题目:(1)是分式的分母分别加上一个常数,为了能够使用基本不等式,我们需要对整式也进行相应的变形;(2)在上一题的基础上,是分式的分子分母不再是一个常数而是二次项,需要分离出一个代数式,变成熟悉的形式;(3)在(1)的情况下分母进一步变化,不是加一个常数,而是混搭的形式;(4)在上一题的基础之上不再是直接观察出结果,而是需要配凑一个系数。【答案】(1)整式变形成113xy,12112132(1)22(13)()(12)1135133133yxxyxyxyxy当且仅当32(1)=13yxxy取等号(2)2222(1)2(1)1(1)2(1)1111212111111xyxxyyxyxyxyxy11111xy然后求当1xy时,代数式1111xy的最小值(3)整式变形成235xyy,求代数式1223xyy最小值(4)假设分式变形为2()(3)xyy的形式,保证x的系数与y的系数之比等于整式中的系数之比,即2==2 3,,1,=2,分式变形为22223xyy整式变形为2234xyy,然后求22223xyy的最小值。例3.(1)已知,xyR,1xy,求12xxy的最小值;(2)已知0,1x,,求121xx的最小值;【解析】这两个题目的变式又不同于之前的形式,(1)主要是分式的一个分子的系数不是一个常数,而是2xy的形式,因为比较接近我们使用基本不等式的形式,所以对另一个分子替换;(2)中好像是缺了整式,但仔细观察不难发现,其实分母之和为定值。【解析】(1)12221122xxyxyxxyxyxy当且仅当2xyyx时取等号(2)因为(1)1xx,然后求121xx的最小值例4.已知0a,0b,21ab,则11343abab取到最小值为.【解析】试题分析:令2(34)(3)(3)(43)abababab,∴131543225,∴111112312(3)34()[(34)(3)][]3433435555343abababababababababab322(3)34322553435abababab,当且仅当212(3)34343ababababab时,等号成立,即11343abab的最小值是3225.例5.已知正数0,0ba满足311ba,求ba的取值范围。解析:方法一:由311ba得abba3,13aab,由于0,0ba,可得31a,于是)31(9131131133113aaaaaaaaba3432)31(91)31(232)31(9131aaaa,当)31(9131aa,即32a时取等号,ba的取值范围是),34[方法二:由311ba得abba3.又2)2(baab,所以2)2(3baba,即4(a b)≤2)(3ba,所以34ba,即ba的取值范围是),34[方法三:由311ba得13131ba,34332323332)3131)((abbaabbabababa,当且仅当abba33,即32ba时取等号,所以ba的取值范围是),34[方法四:由311ba得abba3(1)设tba,则atb,代入(1)式得)(3atat整理得0332ttaa,又由311ba得31a,即方程0332ttaa在),31(上有解,令ttaaag33)(2,则0)31(31323034)3(33)(22gtttttaaag解得34t,所以ba的取值范围是),34[方法五:轮换对称性:因为ba,的地位是样的,当取最值时,ba,在相等的时候取到:322311baba,所以最小值为34方法六:柯西不等式的推论:解:令zbamin,343113111122zzbaba例6.已知,10x求函数xxy1412的最小值令:1243522223522542514141.1132222222yxxyxyyxyxyxxyyxyxxyyxxyxyxyxxyxxxyxyx例7.已知0x,0y,0z,且411yzx,则xyz的最小值为()A.8B.9C.12D.16【解析】由0x,0y,0z得,41()[()]()xyzxyzxyzyzx45xyzyzx4529xyzyzx,当且仅当3,6xyz时等号成立。选B。例8.已知实数,mn,若0,0mn,且1mn,则2221mnmn的最小值为()A.14B.415C.18D.13思路:本题可以直接代入消元解决,但运算较繁琐。考虑对所求表达式先变形再求值,可用分离常数法将分式进行简化。2241212121mnmnmnmn,结合分母可将条件1mn,变形为214mn,进而利用均值不等式求出最值【解析】:222244114121212121mnmnmnmnmnmn4141322121mnmnmn1214mnmn414141112214121214421nmmnmnmnmn41129524214nmmn229122144mnmn,即2221mnmn的最小值为14答案:A二、柯西不等式证明1.对于任意Rdcba,,,恒有不等式22222dcbabdac证明:构造向量2222,,,,dcnbamdcnbam,,cos,nmnmnmnmbdacnm所以得证,当两向量平行时,等号成立。对柯西不等式变形,易得,222yxbayxybxa当ybxa时,等号成立。当然我们也可以构造向量:yxnybxam,,,。证明2.已知,ab为正常数,ab,,0,xy,求证:222ababxyxy≥(权方和不等式)证明:由于a,b,x,y均为正实数,而222222222222abaybxaybxxyabababxyxyxy≥,所以222ababxyxy≥.当且仅当22aybxxy,即abxy时等号成立.推广:若0,0iiba,则nnnnbbbaaabababa212212222121成立。当iiba时,等号成立。若0,0,0mbaii,则mnmnmnmnmmmmbbbaaabababa211211212111成立。当iiba时,等号成立。注意观察,m成为该不等式的权,它的特点是分子的幂指数比分母的幂指数高1次。例1.求函数)20(cos8sin1)(xxxxf的最小值解析:55cossin41cos4sin1cos8sin1)(2122232122321223xxxxxxxf例2.已知,12,,*yxRyx求yx21的最小值()解析:9)2()21(22121221212yxyxyx)(例3.已知Ryx,,且18yx,则2211yx的最小值为A28B64C264D125方法1:权方和不等式:111112121212()()qqqqnnqqqqnnaaaaaabbbbbb得:333222221114(14)125(8)(8)xyxyxy方法2:大柯西不等式:0,0,0iiiabc,则3333121212111222()()()()nnnnnnaaabbbcccabcabcabc322221111(8)(8)()(14)xyxyxyxy方法3:利用导数:110,08xyy,22221111()(18)fyxyyy,3333331622[(2)(18)]()(101)(18)(18)yyfyyyyyy,min1()()12510fyf例4.已知00xy,,且191xy,则xy的最小值是_______.解析:yxyxyx2223131911)(9yx例5.已知0,0yx,且12yx,则yx11的最小值是_______.解析:2232)21(221212111222yxyxyxyx例6.已知0,0yx,且292yx,求yx2的最小值。答案225例7.已知0,0yx,且123yx,求yx23的最小值。答案25例8.求函数291,0,122fxxxx的最小值总结,已知axbyc,求dexy的最小值;或者已知decxy,求axby的最小值.权方和不等式可秒此类题目cbeadbyaxbeadbybeaxadbybeaxadyexd2222)()(byaxbeadbybeaxadbybeaxadyexdc222)(byaxcbead2)(四、因式分解 基本不等式 轮换对称性 参数方程例1.已知0,0ba且3baab,则ba的最小值为()解一:621122114113bababababaab当且仅当:,11ba即3,3ba时6minba解二:(参数方程)解三:轮换对称性。解四:令61cot21tan2,1cot2,1tan2cot21,tan21bababa.例2.已知正实数,xy满足24xyxy,则xy的最小值为__________解:24xyxy得:6)2)(1(42yxyxxy,令cot62,tan61yx得:3622cot61tan6yx五、几个重要基本不等式以及万能Δ法(1)若aR,则20,0aa;(2)若,abR,则222abab(当且仅当ab时等号成立);(3)若,,abR则2abab(当且仅当ab时等号成立)—基本不等式推广:若,,abR则2221122abababab;当且仅当ab时等号成立;应用:设,,abR则“积为定值和有最小值”,“和为定值积有最大值”。注意:“一正二定三相等”例1.已知,12yx求22yxx的最小值()解法一:令5404012222222222222mmmmmmmyyymymmymxmyxx解法二:sincos21coscossincos21,1sincos2sin,cosrrrrrryrx;451cos2sin21cos2sin2cos21cossincos2也可三角函数求值域541121cos12sinsincos21cos22mmmmmm例2.设,5,0,0baba则31ba的最大值()解法一:23231231baba解法二:3,1;9,1,133,112222yxyxybxaybxa圆心到直线yx的距离,23,32yxtrtd当且仅当,yx即23,27,31baba例3.已知0,0xy,且115xyxy,则xy的最大值是________思路:本题观察到所求xy与11xy的联系,即2114112xyxyxyxy,代入方程中可得:245540xyxyxyxy,解得:14xy,所以最大值为4。答案:4例4.已知20ab,则4(2)abab的最小值为______________思路一:所求表达式为和式,故考虑构造乘积为定值以便于利用均值不等式,分母为2bab,所以可将a构造为112222aabb,从而三项使用均值不等式即可求出最小值:341818(2)3(2)3(2)2(2)2(2)aabbabbbabbabbab思路二:观察到表达式中分式的分母2bab,可想到作和可以消去b,可得2222babbaba,从而244(2)aababa,设24faaa,可从函数角度求得最小值(利用导数),也可继续构造成乘积为定值:32244332222aaaafaaa。答案:3例5.已知ab,且1ab,则22abab的最小值是解析:222222222abaabbabababab例6.已知,0,ab,且21ab,则2224sabab的最大值是()A.212B.21C.21D.212解析:22222222ababab,222222142222ababab22142ab212s六、不等式精选试题1.以下基本不等式最值为什么错误?说明理由()(1)4424xxxxy(2)2,032sin3sin2sin3sinxxxxxy(3)4104loglg2104loglgxxxxy2.已知0,yx且42yx,则12yx的最大值是(3)3.已知0,yx且42yx则yx12的最小值是(2)4.已知0,ba且12ba则baba31431的最小值是(5223)5.已知0cba则cabbaabca1112的最小值是(6)6.已知52322ba,则21222bay最大值是(437)7.已知0,yx且12yx,则224131yxyxyx最小值是(4)8.已知0,yx且1019yxyx,则yx的最大值是()解析:82yx9.已知0cba,则2296442cacbaaaba的最小值为(D)A.4B.5C.52D.8解析:21614144abababaaab,后用均值不等式10.已知0,ba且111ba则1911ba的最小值是(6)11.若正数ba,满足112ba,则1324ba的最小值是(D)A.4B.23C.32D.6211.已知Rba,且2ba则111122ba的最大值是(1)12.已知0,yx且419211yxyx则yx1673的最小值是(41)解析:414192916732916734191673211yxyxyxyxyx13.已知21,1yx不等式114122222xayyax恒成立,则实数a的最大值为(4)14.已知实数yx,满足1422xyyx,则yx2的最大值是(5102)15.已知正实数yx,满足xyyx62,则xy的最小值是(18)16.已知实数cba,,满足1,0222cbacba,则a的最大值是(36)17.已知实数yx,满足545422yxyx,设22yxS则minmax11SS(58)18.已知,1222zyx则yzxy3的最小值法一、令sinsincossincoszyx1,13sin2sin3yzxy法二、131114432222222yzxyyyzyyxyzxy法三、令181,84,8381,84,83818483023|,,;02|,,;023|,,3,,min222222fffzyxyzxzyxfzyzyxfxyzyxfzyxyzxyzyxfyyx19.已知BA,是函数xy2的图像上的相异两点,若点BA,到直线21y的距离相等,则点BA,的横坐标之和的取值范围是(B)A.1,B.2,C.3,D.4,20.函数Inxxf,若ba0,且bfaf,则ba的取值范围,221.函数xxflg,若ba0,且bfaf,则ba2的取值范围,322.xxxf2cos14sin3的最大值为4123.已知,,Ryx62322yx,则yx2的最大值为(11),最小值为(11)24.已知正数yx,满足22yxxy,则yx的最小值为()325.已知yx,满足4yxxy,则yx的最小值为(32)26.小题训练1.若a,b,c为实数,则下列命题为真命题的是()A.若ab,则22acbcB.若0ab,则22aabbC.若0ab,则11abD.若0ab,则baab2.不等式|5||3|10xx的解集是()A.[5,7]B.[4,6]C.(,5][7,)D.(,4][6,)3.下列不等式:①12xx;②1||2xx;③若01ab,则loglog2abba;④若01ab,则loglog2abba.其中正确的是()A.②④B.①②C.②③D.①②④4.若,xyR且满足32xy,则3271xy的最小值是()A.339B.122C.6D.75.若直线22221(0,0)xyabab过点(1,1),则ab的最小值等于()A.2B.3C.4D.56.对于实数x,y,若|1|1x,|2|1y,则|21|xy的最大值为()A.1B.2C.4D.57.已知,abR,且1ab,则2()Paxby与22Qaxby的关系是()A.PQB.PQC.PQD.PQ8.若函数()|1||2|fxxxa的最小值为3,则实数a的值为()A.5或8B.1或5C.1或4D.4或89.已知abc,若11nabbcac,则n的最大值为()A.3B.4C.14D.810.设1x,则(5)(2)1xxyx的最小值为()A.4B.9C.7D.1311.已知正数x,y满足1xy,则11()()zxyxy的最小值为()A.2(21)B.4C.254D.812.若实数x,y满足221xyxy,则xy的范围是()A.2(3,)3B.[6,)C.22[3,3]33D.3(,]413.设x,y时满足24xy的正数,则lglgxy的最大值是.14.已知关于x的不等式|1|||1xxc无解,实数c的取值范围.15.若不等式|3|4xb的解集中的整数有且仅有321,,则b的取值范围为.16.若正实数x,y满足244xyxy,且不等式2(2)22340xyaaxy恒成立,则实数a的取值范围是.答案:1-5:BDCDC6-10:DADBB11、12:CC13.lg214.(,0][2,)15.(5,7)16.5[,3][,)217.已知正实数ba,满足1ba,则222124abab的最小值为_______.【解析】【分析】对222124abab变形为222124142ababab,再转化为222124142abababab,利用基本不等式即可求得最小值,问题得解。【详解】因为1ab,且,ab都是正实数.所以2221241414222ababababab14144421277211babaababababab当且仅当12,33ab时,等号成立.所以222124abab的最小值为1118.已知正实数x,y满足141223xyxy,则xy的最小值为______.【答案】94构造有关的等式关系.yx=12234xyxy,利用基本不等式的性质即可解决.【详解】12xy 423xy1,yx=12234xyxy,那么:1)(yxyx=12234xyxy×(12xy 423xy)=14(1 42234232xyxyxyxy)=522342342xyxyxyxy∵2231223424xyxyxyxy=1,当且仅当yx2=32时取等号.所以:yx≥59144.故yx的最小值为94.故答案为:9419.已知0a,0b,且23abab,则ab的最小值是__________.【解析】因为23abab23226abab,当且仅当23ba时取等号.因此ab的最小值是26.20.已知正实数cba,,满足111ab,111abc,则c的取值范围是_____.【答案】4(1,]3【解析】由11ab=1,可得1bab,由111abc,得111111121cabbb,1121bb,11014121bb,3114c,413c,故答案为41,3.21.(2019·陕西省商丹高新学校期末(理))已知0x,0y,若2282yxmmxy恒成立,则实数m的取值范围是()A.4m≥或2mB.2m或4mC.42mD.24m【答案】C22.(2020·湖南长沙·长郡中学期末)函数1(3)3yxxx的最小值为()A.5B.3C.2D.5【答案】A23.(2020·陕西商洛·期末(文))已知,ab为正数,2247ab,则21ab的最大值为()A.7B.3C.22D.2【答案】D24.(2020·吉林洮北·白城一中期末(理))若直线10axby,(a,0b)过点2,1,则11ab的最小值为()A.322B.8C.42D.322【答案】D25.(2020·湖北期中)已知0x,0y,且23xyxy,则2xy的最小值是()A.3B.22C.322D.83【答案】D26.(2020·安徽宣城·月考(文))若0a,0b,112ab,则4ab的最小值为()A.92B.4C.72D.3【答案】A27.(2020·安徽宣城·月考(理))已知0x,0y,22xyxy,若xay的最小值为8,则正实数a的值为()A.2B.32C.3D.92【答案】D28.(2020·安徽月考)若实数)1,0(,ba,且41ab,则ba1211的最小值()解析:3244214)24(214244421421141121141412aaaaaaabab29.(2020·蚌埠田家炳中学开学考试)求函数222163xxy的最小值()解析一:61386364863364832163222222xxxxxx解析二:6138631631631662316231623162222163622222222xxxxxxxx30.(2020·湖北襄城·襄阳四中其他(理))设0a,0b,lg2是lg4a与lg2b的等差中项,则21ab的最小值为()A.22B.3C.4D.9【答案】D31.(2020·黑龙江尖山·双鸭山一中期末(文))已知2212,202bmaanba()(),则nm,之间的大小关系是()A.nmB.nmC.nmD.不确定【答案】C32.(2020·运城市景胜中学期末)已知0a,0b,1ab,则11ab的最小值为______.【答案】433.(2020·重庆北碚·西南大学附中期末)已知xy,为正实数,则22xxyxyx的最小值为_________.【答案】32234.(2020·重庆北碚·西南大学附中期末)已知向量2,1ay,,3bx,且ab,若x,y均为正数,则32xy的最小值是______.【答案】835.(2019·陕西省商丹高新学校期中(文))设正数,xy满足222log(3)loglogxyxy,则xy的取值范围是_____.【答案】6,36.(2020·沙坪坝·重庆一中期末)设x,y为正实数,若2241xyxy,则266xyxy的最大值是______.【答案】101837.(2020·重庆市凤鸣山中学月考)已知0a,0b,下面四个结论:①22ababab;②2222abab;③若ab,则22ccab;④若11111ab,则2ab的最小值为22;其中正确结论的序号是______.(把你认为正确的结论的序号都填上)【答案】①③④38.(2020·沙坪坝·重庆八中期末)已知0m,0n,且111223mn,则2mn的最小值为________.【答案】36239.(2020·湖北期中)已知,abR,250ab则24ab的最小值等于________.【答案】8240.(2020·湖北襄阳·期中)已知32x,则1()4146fxxx的最小值为______.【答案】741.(2020·湖南省长沙县第九中学期末)已知0x,0y,且211xy,若227xymm恒成立,则实数m的取值范围是______.【答案】1,842.(2020·安徽定远·期中)已知0a,0b,且22ab,那么21ab的最小值为________.【答案】4.43.(2020·河南平顶山·期末(文))若正实数,xy满足39loglog1xy,则2xy的最小值为_____.【答案】6;44.(2020·黑龙江龙凤·大庆四中月考(理))已知0x,0y,1411xy,则xy的最小值为______.【答案】845.(2020·湖北荆门外语学校期中)设02x,则912xx的最小值为_________.【答案】8七、不等式的基本计算与不等式的基本性质1.不等式的基本计算一、一元一次不等式的解法任何一个一元一次不等式经过不等式的同解变形后,都可以化为(0)axba的形式.当0a时,不等式的解集为bxxa;当0a时,不等式的解集为bxxa.二、一元二次不等式20(0)axbxca的解法1、二次不等式2()0fxaxbxc(0a)的解法:最好的方法是图像法,充分体现了数形结合的思想.也可以利用口诀(大于取两边,小于取中间)解答.2、当二次不等式()fx20(0)axbxca时,可以画图,解不等式,也可以把二次项的系数a变成正数,再利用上面的方法解答.3、温馨提示(1)不要把不等式20axbxc看成了一元二次不等式,一定邀注意观察分析2x的系数.(2)对于含有参数的不等式注意考虑是否要分类讨论.解决含参数不等式的难点在于对参数的恰当分类,关键是找到对参数进行讨论的原因,确定好分类标准,有理有据、层次清楚地求解.(3)如果运用口诀解一元二次不等式,一定要注意使用口诀必须满足的前提条件.(4)不等式的解集必须用集合或区间,不能用不等式,注意结果的规范性.三、指数不等式和对数不等式的解法解指数不等式和对数不等式一般有以下两种方法(1)同底法:如果两边能化为同底的指数或对数,先化为同底,再根据指数、对数的单调性转化为代数不等式,底数是参数时要注意观察分析是否要对其进行讨论,并注意到对数真数大于零的限制条件.①当1a时,:()()()()fxgxaafxgx;()0log()log()()0()()aafxfxgxgxfxgx②当01a时,:()()()()fxgxaafxgx;()0log()log()()0()()aafxfxgxgxfxgx(2)对指互化法:如果两边不能化成同底的指数或对数时,一般用对指互化法.对数不等式两边取指数,转化成整式不等式来解;指数不等式两边取对数,转化成整式不等式来解.(1)xabalog()loglogxaaaabxb,(01)xabalog()loglogxaaaabxblog00log(1)aaxbxxxbaxbaa其中,log00log(1)aaxbxxxbaxbaa其中0四、分式不等式的解法把分式不等式通过移项、通分、因式分解等化成()0()fxgx的形式→化成不等式组()0()()0gxfxgx→解不等式组得解集.(温馨提示:解分式不等式一定要考虑定义域.)五、高次不等式的解法先把高次不等式分解因式化成123()()()()0nxaxaxaxa的形式(x的系数必须为正)→标记方程的实根(注意空心和实心之分)→穿针引线,从右往左,从上往下穿(奇穿偶不穿)→写出不等式的解集.实际上,序轴标根法适用于所有的整式不等式,根据它可以很快地写出整式不等式的解集.六、绝对值不等式的解法方法一:公式法解只含有一个绝对值形如()axbc的不等式,一般直接用公式xaxaxa或xaaxa,注意集合的关系和集合的运算,集合的运算主要利用数轴.方法二:零点讨论法解含有两个绝对值形如()xaxbc的不等式,常用零点讨论法和数形结合法.注意小分类求交大综合求并.方法三:平方法如果绝对值的不等式的两边都是非负数,如:3x,可以使用平方法.七、无理不等式的解法无理不等式一般利用平方法和分类讨论解答.无理不等式转化为有理不等式,要注意平方的条件和根式有意义的条件,一般情况下,)()(xgxf可转化为)()(xgxf或)()(xgxf,而)()(xgxf等价于:0)(0)(xgxf或2)]([)(0)(0)(xgxfxgxf.八、抽象的函数不等式的解法一般利用函数的单调性解答,先研究函数的单调性,再利用函数的单调性把抽象的函数不等式转化成具体的函数不等式解答.2.不等式的性质(1)实数的大小比较与实数运算性质之间的关系:0abab;0abab;0abab(2)不等式的基本性质性质1.(传递性)如果,abbc,那么ac性质2.(加法性质)如果ab,那么acbc性质3.(乘法性质)如果ab,0c,那么acbc;如果ab,0,c那么acbc(3)从不等式的基本性质出发,还可以得到哪些有用的推论?推论1.,abcdacbd如果那么;推论2.,abcdacbd如果那么推论3.0,0abcdacbd如果那么;推论4.110,abab如果那么推论5.0,0ababdccd如果那么;推论6.*0,()nnababnN如果那么推论7.110,nnabab如果那么*(,1)nNn(4)如何比较不等式的大小?①作差法②作商法不等式证明的常用方法:(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;(2)作商(常用于分数指数幂的代数式);(3)分析法;(4)平方法;(5)分子(或分母)有理化;(6)利用函数的单调性;(7)寻找中间量或放缩法;(8)图象法.其中比较法(作差、作商)是最基本的方法.(一).不等式的解法练习题1.(2020·运城市景胜中学期末)不等式111x的解集为()A.(,0][1,)B.[0,)C.(,0](1,)D.[0,1)(1,)【答案】C2.(2020·黑龙江龙凤·大庆四中月考(理))不等式102xx的解集为()A.[1,2]B.[1,2)C.(,1][2,)D.(,1)(2,)【答案】B3.(2020·全国开学考试)不等式321xx的解集是()A.|15xxB.|15xxC.|15 xxD.|15 xx【答案】A4.(2020·江苏淮阴中学期末)不等式2411xxx的解集为()A.1x或3xB.1x或13xC.11xx或3xD.11xx或13x【答案】C5.(2020·安徽屯溪一中高一期中)不等式3112xx的解集是()A.324xxB.324xxC.{3|4xx或2}xD.2xx【答案】B6.(2020·湖北蔡甸·汉阳一中高三其他(理))已知集合4{|0}1xAxRx2{|(2)(1)0}BxRxaxa,若AB,则实数a的取值范围是()A.(2,)B.[2,)C.1[2,)D.(1,)【答案】C7.(2020·全国高三二模(文))已知集合306xAxx,23100Bxxx,则RABð()A.,35,B.,35,C.,35,D.,35,【答案】A8.(2020·浙江省平阳中学高三一模)若集合2|0,|121xAxBxxx,则AB=()A.[2,2)B.(]1,1C.11,D.12,【答案】C9.(2020·朝阳·吉林省实验高一期末)不等式222221xxxx的解集为()A.2xxB.RC.D.|2xx或2x【答案】A10.(2020·长春市第一中学高二期中(文))已知集合1|02xAxx,|12Bxx,则AB()A.(1,2)B.(1,2]C.1,2D.[1,2)【答案】A11.(2020·全国高三其他(理))已知集合11Mxx,2230Nxxx,则MN()A.B.1,0C.1,3D.1,01,3【答案】D12.(2020·全国开学考试)不等式234023xxxxx的解集为_________.【答案】,31,02,4.13.(2020·安徽蚌埠·期末)不等式25601xxx的解集为____________.【答案】(1,2)(3,)14.(2019·江西新余·高二期末(文))设关于x的不等式0axb的解集为2xx,则关于x的不等式2056axbxx的解集为______.【答案】,12,615.(2020·浙江高一课时练习)不等式111xx的解集是__________.【答案】{2xx|或21}x.16.(2020·全国开学考试)不等式252(1)xx的解集是.【答案】3,11,2117.(2020·河北省临西县实验中学期末)若关于x的不等式220axax的解集为R,则a的取值范围为()A.0,4B.0,4C.0,8D.0,8【答案】D18.(2020·湖北襄阳·期中)设一元二次不等式220axbx的解集为|24xx,则ab的值为()A.14B.18C.8D.12【答案】B19.(2019·陕西省商丹高新学校期末(理))不等式210xmx的解集为空集,则m的取值范围是()A.(-2,2)B.[-2,2]C.(,2)(2,)D.(,2][2,)【答案】B20.(2020·湖北期中)若不等式202211xmxm有唯一解,则实数m的取值为()A.0B.1C.0或2D.1或3【答案】C21.(2020·安徽宣城·月考(文))函数2()76fxxx的定义域为()A.[1,6]B.(,1][6,)UC.[6,1]D.(,6][1,)U【答案】B22.(2019·黑龙江龙凤·大庆四中月考(文))若函数2()21fxmxmx的定义域为R,则实数m的范围是()A.0,1B.0,1C.0,1D.,01,【答案】A23.(2020·安徽宣城·月考(理))关于x的不等式2450xx的解集为()A.(5,1)B.(1,5)C.(,5)(1,)D.(,1)(5,)【答案】B24.(2020·安徽月考)不等式220xx的解集为()A.1,2B.2,1C.1,2D.【答案】D25.(2020·四川成都·期末(理))二次不等式20axbxc的解为全体实数的条件是()A.00aB.00aC.00aD.00a【答案】B26.(2020·黄梅国际育才高级中学期中)在R上定义运算☉:A☉B=A(1-B),若不等式xa☉1xa对任意的实数x∈R恒成立,则实数a的取值范围为()A.11aB.02aC.1322aD.3122a【答案】C27.(2020·全国开学考试)若关于x的一元二次方程0122xax无解,则a的取值范围是()A.),1(B.)1,(C.,1D.),0()0,1(.【答案】B28.(2020·宁夏银川二中期末)如果关于x的不等式2xaxb的解集是{|13}xx,那么ab等于()A.-81B.81C.-64D.64【答案】B29.(2020·湖北省汉川市第一高级中学期末)设函数2()1fxmxmx,若对于任意的x∈{x|1≤x≤3},()4fxm恒成立,则实数m的取值范围为()A.0mB.750mC.0m或750mD.75m【答案】D30.(2020·江苏省海州高级中学月考)不等式2340xx的解集为()A.,41,UB.,14,C.4,1D.1,4【答案】C31.(2020·江苏如皋·期末)关于x的不等式22140xmxm的解集中恰有4个正整数,则实数m的取值范围是()A.5,32B.5,32C.11,2D.151,,322【答案】B32.(2020·安徽庐江·期末)若关于x的不等式20xpxq的解集为{|23}xx,则关于x的不等式22028xpxqxx的解集是()A.2,3B.,24,C.2,23,4D.,22,34,【答案】D33.(2020·广东梅州·其他(理))已知集合220Axxx,12Bxx,则AB()A.12,3B.2,3C.1,3D.11,3【答案】A34.(2020·全国课时练习)不等式2x2-x-1>0的解集是()A.112xxB.1|xxC.2,1|xxxD.12xx或1x【答案】D35.(2019·广州市培正中学期末)已知不等式210axbx的解集是1123xx,则不等式20bxxa的解集是()A.23xxB.32xxC.322xxD.1132xx【答案】A36.(2017·安徽淮北·高三其他)若122xx,则13xx的取值范围是()A.0,3B.4,3C.4,0D.3,4【答案】C37.(2020·黑龙江松北·哈九中高三三模(理))已知集合{ln(1)}Mxyx∣,220Nxxx∣,则MN()A.0,2B.0,1C.,1D.,2【答案】D38.(2020·黑龙江绥化·(理))已知集合2{|230}Pxxx,{|14}Qxx,则R()PQð等于()A.(1,1]B.(3,4]C.(,1)[1,)D.(,1)(3,)【答案】A39.(2020·黑龙江龙凤·大庆四中高一月考(文))关于x的不等式0axb的解集是(1,),则关于x的不等式()(3)0axbx的解集是()A.(,1)(3,)B.(1,3)C.(1,3)D.(,1)(3,)【答案】A(二).不等式的基本性质习题1.(2020·河北省临西县实验中学期末)已知ac,bd,则下列结论正确的是()A.22()()abcdB.0abcdadbcC.abcdD.abcd【答案】B2.(2020·安徽宣城·期中)已知2tab,21sab,则t和s的大小关系为()A.tsB.tsC.tsD.ts【答案】D3.(2020·安徽宣城·期中)设a、b、c为实数,且0ab,则下列不等式正确的是()A.2aabB.22acbcC.baabD.11ab【答案】D4.(2020·湖南长沙·长郡中学期末)已知0ab,则下列不等式中正确的是()A.abB.11abC.abD.22ab【答案】B5.(2020·沙坪坝·重庆八中期末)如果实数m,n,满足:0mn,则下列不等式中不成立的是()A.mnB.11mnmC.11nmD.220nm【答案】B6.(2020·湖北期中)如果aR,0bc,则下列不等式正确的是()A.22abacB.0abacC.11caD.11cb【答案】D7.(2020·湖北襄阳·期中)下列命题中,正确的是()A.若acbc,则abB.若ab,cd,则acbdC.若0ab,则22abD.若ab,cd,则acbd【答案】C8.(2020·广东梅州·期末)若ab,则下列不等式中正确的是()A.22abB.11abC.222ababD.22acbc【答案】C9.(2020·安徽宣城·月考(文))若实数a,b满足0ab,则下列正确的结论为()A.22abB.2abaC.2babD.ln()ln()ab【答案】D10.(2020·包头市第九中学期末)下列命题为真命题的是()A.若0ab,则22acbcB.若0ab,则22abC.若0ab,则22aabbD.若0ab,则11ab【答案】B11.(2020·湖南省长沙县第九中学期末)设0ab,下列不等式一定成立的是()A.22aabbB.22babaC.22ababD.22abba【答案】B12.(2020·邯郸市永年区第一中学期末)已知a,b,c,d为实数,ab且cd,则下列不等式一定成立的是().A.acbdB.acbdC.adbcD.11ab【答案】C13.(2020·湖北荆门外语学校期中)已知0ba,则下列不等式成立的是()A.22abB.11abC.11babD.2aba【答案】C14.(2020·日喀则市第三高级中学期末(理))设11ab,则下列不等式中恒成立的是()A.11abB.11abC.2abD.22ab【答案】C15.(2020·四川成都·期末(理))下列四个说法中,错误..的是()①若a,b均为正数,则112abab②若π0,2x,则1sinsinxx的最小值为2③若1ab,则11bbaa④0ab,则11abbaA.①②③B.①③C.②③D.②④【答案】C16.(2020·四川成都·期末(理))若abc,则下列说法正确的是()A.lnlnabB.22abC.11cacbD.1122ab【答案】C17.(2020·黄梅国际育才高级中学期中)下列结论正确的是().A.若acbc,则abB.若22ab,则abC.若ab,0c,则acbcD.若ab,则ab【答案】C18.(2020·临猗县临晋中学月考)如果0ba,那么下面一定成立的是()A.bcacB.0baC.22baD.1a<1b【答案】C19.(2020·上海开学考试)实数a、b在数轴上的对应点的位置如图所示,下列关系式不成立的是()A.55abB.66abC.abD.0ab【答案】C20.(2020·梅河口市第五中学月考)设,0abc,则下列结论中正确的是()A.ccabB.11acbcC.acbcD.22acbc【答案】D21.(2020·宁夏银川二中期末)若,,abc为实数,则下列命题错误的是()A.若22acbc,则abB.若0ab,则22abC.若0ab,则11abD.若0ab,0cd,则acbd【答案】B22.(2020·黑龙江南岗·哈师大附中期末)若ba,则下列各式中正确的是()A.bcacB.22bcacC.22cbcaD.11ab<【答案】C23.(2020·安徽池州·期末(文))若1ab,则下列不等式中不一定成立的是()A.1abbB.11abC.1abaD.11ab【答案】D24.(2020·黑龙江龙凤·大庆四中月考(文))若0ab,则下列不等式中不能成立的是()A.11abB.11abaC.||||abD.33ab【答案】B25.(2020·湖南岳阳·期末)对于任意实数ba,,若ba,则下列不等式一定成立的是()A.11abB.22baC.33baD.abba【答案】C26.(2020·湖北茅箭·十堰一中月考)已知0ab,则下列不等式成立的是()A.2abababB.2abaabbC.2abababD.2abaabb.【答案】B27.(多选题)(2020·福建厦门·期末)已知abc,则下列不等式一定成立的是()A.2abcB.abbcC.acbcD.11acbc【答案】AD28.(多选题)(2020·江苏如皋·期末)若0ab,则下列结论正确的是()A.11aabB.baabC.2211abD.22aabb【答案】AD29.(2020·胶州市教育局期末)若1ab,01c,则()A.ccabB.ccabbaC.loglogbaacbcD.loglogabcc【答案】C30.(2020·全国高二课时练习)已知直线1xyab经过第一、二、三象限且斜率小于1,那么下列不等式中一定正确的是()A.abB.abC.0babaD.11ab【答案】B31.(2020·湖南开福·长沙一中高三月考(理))若110ab,则下面四个不等式恒成立的是()A.ababB.ababC.||||abD.33ab【答案】A32.(2020·浙江省杭州第二中学高三其他)若0ab,则()A.lnln0abB.330abC. tantan0abD.ab【答案】B33.(2020·陕西高三其他(理))若0ba,则下列结论不正确的是()A.11abB.2abaC.||||||ababD.33ab【答案】C34.(2020·四川武侯·成都七中高一期末)设ab,则下列不等式一定成立的是()A.abB.11abC.22abD.22ab【答案】D35.(2020·上海高三专题练习)设cba,,是互不相等的正数,则下列等式中不恒成立的是()A.||||||abacbcB.2211aaaaC.1||2ababD.312aaaa【答案】C36.(2020·上海高三专题练习)设,abR,若bbmaam(m为大于0的常数)成立,则().A.abB.abC.abD.ab【答案】A37.(2020·绥德中学高三其他(理))若0x,0y,则下列不等式一定成立的是()A.222xyxB.1222log1xyxC.222yxxD.1222log1yxx【答案】B38.(2020·陕西安康·高三其他(文))已知定义在R上的函数sinxxxf,正实数,,abc满足cabfffabbcca,则()A.cbaB.abcC.cabD.acb【答案】C39.(2020·北京东城·高三一模)已知1x,那么在下列不等式中,不成立的是()A.210xB.12xxC.sin0xxD.cos0xx【答案】D
,
琴生不等式和柯西不等式(柯西不等式与holder不等式)
阅读全文>>2022-11-03 13:21:01
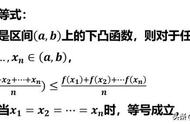
琴生不等式背景是什么(什么是琴生不等式)
阅读全文>>2022-11-03 12:52:07

凹凸不等式也叫琴生不等式吗(高一不等式100道题)
阅读全文>>2022-11-03 13:24:30

28个著名不等式(高一不等式恒成立的八种解题模型)
阅读全文>>2022-11-03 13:01:56

琴生不等式(琴生不等式使用套路)
阅读全文>>2022-11-03 13:37:07

十大经典不等式(柯西不等式6个基本题型)
阅读全文>>2022-11-03 13:17:58
数学史上浪漫数学公式(数学史上最美的公式)
阅读全文>>2022-11-03 13:25:55

拉格朗日秒杀高考例题(拉格朗日乘数法)
阅读全文>>2022-11-03 13:12:23

琴生不等式背景(琴生是如何证明琴生不等式的)
阅读全文>>2022-11-03 12:54:39
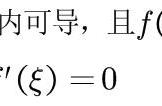
罗尔定理秒杀高考(罗尔定理解决高中数学题)
阅读全文>>2022-11-03 13:13:49





