“什么是周长”这一内容,教材选择用树叶这样不规则的图形及学生熟悉的数学书封面这样规则的图形引入,帮助学生逐步建立周长的概念。实物图形抽象出来是几何图形,教材没有直接给出规则的几何图形,意图是让学生有充分的时间和空间、有充实的活动先理解周长的意义。如果第一节就学习规则的平面图形的周长,过早地形式化,就有可能导致学生对周长的理解只是一些公式,如果这样对周长的理解是不全面的。从实物图形出发,还有一点就是周长的产生本身来源于实践,应该让学生意识到不仅仅抽象的图形有周长,实际生活中到处都有周长的应用。
此外,教材引导学生通过看、描、量、数等系列操作活动,让学生直观地体验和感受周长的实际意义。这样的活动在教学过程中是必不可少的。

四年级上册︱以前利用运算律进行简算是一个重要内容,现在教材有所削弱,教材是怎样处理的?为什么要这样做?
这样做主要是基于运算律价值的思考。运算律的学习,对学生来说非常重要。加法和乘法中的五个运算律是所有运算的基础,学习运算律不仅仅是为了计算的简便,更为重要的是,帮助学生发展对于数的意义和运算意义的理解。运算律本身既是算理,也体现了运算的本质(算式的等值变形)。所以本册教材对学习运算律的价值重新定位:一是把运算律作为探究的素材,利用学生的生活经验和知识基础,让学生去观察与猜想,用数据去验证、归纳规律并应用,经历通过对算式的研究,培养学生发现与提出、分析与解决问题的能力;二是应用运算律能进行一些简便计算,控制计算的复杂性与技巧,意在培养简便运算意识的同时,突出对运算意义本身的理解。
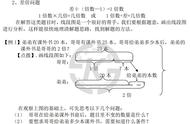
为突出对学生发现与提出、 分析与解决问题能力的培养,教材在内容编排上具有如下特点:首先,由于两个交换律和两个结合律分别具有相通与相似的地方,放在一起或连着进行编排,更容易发现规律;其次,基本上都是以数学问题引入,直接聚焦对多个算式本身所具有特点的研究,更有助于对规律的归纳与概括;重要的是精心设计问题串,使 5 个运算律内容的结构基本一致,形成了观察仿写算式—解释规律—表述规律—应用规律的呈现特点(如下图)。观察与仿写算式,就是引导学生初步发现问题与提出问题;解释规律,就是结合事例,通过图示(方块图、线段图、点子图等)体现数形结合,直观地解释初步的发现,最后确认发现的问题,为归纳一般性的规律(提出问题)奠定基础;用字母表述规律,就是一个由具体数值计算到符号表达的过程,完成了由几个特例的共性特点归纳概括出一般性的结论,从而简练清晰地提出问题;应用规律,就是运用规律具体分析算式特点,把算式进行等值变形使运算简洁合理,即分析与解决问题。所以说,内容的编排与问题的设计,让学生很好地经历“发现和提出、分析和解决问题“的全过程,为培养创新能力而积累推理的数学活动经验。


五年级上册︱教材为什么没有出现“互质数”的概念?
首先,学生理解互质数的概念比较困难。
从互质数的概念来看,互质的两个数不一定是质数,如,4 和 9 也是互质数,虽然 4 和 9 都是合数。这与我们平时“起名字”的习惯有很大的不同。我们说正整数,一定符合是“正数”“整数”“数”这几个条件,决不会像互质的两个数掺进另类的“合数”来。
其次,小学阶段学习互质数并不是必要的。
有的教师提出,不学互质数,那么怎么教学最简分数呢?教材对于最简分数的处理是描述性的(见图 1)。在这里,没有用互质数来说明什么是最简分数。在实际的教学中,教师们反馈学生能够理解最简分数,也不存在困惑。