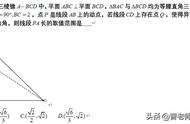
如图,在三棱锥ABC﹣A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.
(1)求证:AB=BC;
(2)若∠ABC=90°,求A1B与平面BCC1B1所成角的正弦值.



考点分析:
直线与平面所成的角.
题干分析:
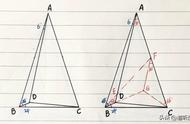
(1)取AC的中点O,连接OA1,OB,推导出AC⊥OA1,AC⊥A1B,从而AC⊥平面OA1B,进而AC⊥OB,由点O为AC的中点,能证明AB=BC;
(2)以线段OB,OC,OA1所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系O﹣xyz,利用向量法能求出A1B与平面BCC1B1所成角的正弦值。
解题反思:
空间角的问题一直是高中数学立体几何部分的重点与难点问题,同时也是高考立体几何解答题部分的热点问题。线线角、线面角、二面角是高考考查的重点知识,三类角号称"三角",而线面角又是重中之重。求线面角的方法源于定义,而又超越于定义。其实线面角就是斜线和它的射影所成的线线角,也是直线与平面的垂线所成角的余角。
直线与平面所成的角是立体几何中的一个重点,也是历年高考的热点。要会求直线与平面所成的角应先弄清楚定义,即直线与平面所成的角是直线和它所在平面内的射影所成的角。
,