平面几何中的“角格点”问题,既有难度、又有趣味;既有规律、又有技巧;外形简精明了、内含丰富知识;今举经典难题一例,说说其的三种解法:
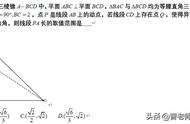
【例题】(如图)在△ABC中,点D为其内一点,且有:AB=AC,∠DAB=6º,∠DBA=48º,∠DBC=24º,求:∠BCD的度数

【思路一】(造内心、导相似比、寻相似)
(1)由题意可得:∠BAC=36º,∠ACB=72º,∠DAC=36º-6º=30º
(2)作∠ABD的平分线交AD、AC分别于点E、F,∴∠ABF=∠FBD=24º=∠DBC,∴∠BFC=60º
(3)作∠ACB的平分线交BD的延长线于点G,点G为△FBC的内心,连FG,∴FG平分∠BFC,∴∠BFG=∠GFC=30º=∠DAC,∴FG∥AD
(4)易证:△ABF∽△CBG,∴AB/BC=BF/BG
(5)由FG∥AD得:BF/BG=BE/BD
(6)得:AB/BC=BE/BD,又∠ABE=∠CBD,∴△ABE∽△CBD,∴∠BCD=∠BAD=6º
【思路二】(正弦定理、导线段比、定相似)

(1)作∠ABD的平分线交边AD于一点E,则:∠ABE=∠EBD=24º,∠BED=30º,∠BDE=126º
(2)由已知可得:∠BAC=36º,∠BCA=72º
(3)根据正弦定理在△BDE和△ABC中可得:BE/BD=sin126º/sin30º=2sin126º=2sin54º;AB/BC=sin72º/sin36º=2cos36º=2sin54º
(4)得:BE/BD=AB/BC,又∠ABE=∠CBD,∴△ABE∽△CBD,∴∠BCD=∠BAE=6º
【思路三】(作外接圆和正三角形构造全等)

(1)由已知可得:∠BAC=36º,∠ACB=72º
(2)作△ABD的外接圆⊙O,连接半径可得:OA=OB=OD,得:∠BOD=12º,∠AOD=96º,∠AOB=108º,∠OAB=∠OBA=36º
(3)由∠AOB+∠ACB=108º+72º=180º,得:AOBC共圆,∵∠OAB=36º=∠BAC,∴OB=BC
(4)以BD为边在△OBD内作正△BDE,连OE,易证:△BOE≌△DOE,∴∠BOE=12º/2=6º
(5)在△BOE中,∠OBE=84º-60º=24º,易证△BOE≌△BCD(SAS),∴∠BCD=∠BOE=6º
以上三种思考方法,“道听度说”供参考。