在圆这一章中,有五个重要考点需要掌握,无论在平时的大小考试中,还是中考,都是热点。

在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等。现在课本中主要介绍的为圆心角、弦和弧三者之间的关系,其实弦心距也是相等的,可以通过全等三角形进行证明。
我们可将之进行推广,在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量对应相等,那么它们所对应的其余各组量都分别相等。
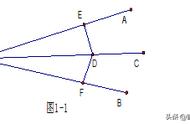
例题1:如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:AE=CE.

解法一:由AB=CD知弧AB=弧CD,同时减去弧AC得到弧AD=弧BC,同圆中同弧所对的弦相等得AD=BC,结合∠ADE=∠CBE,∠A=∠C通过“ASA”可证△ADE≌△CBE,从而得出答案.
解法二:根据我们上一篇讲的连接法构造全等三角形,可连接线段AC或BD,证明△ABC≌△CDA(SSS),得∠BAC=∠ACD,根据等角对等边得AE=CE.

本题主要考查圆心角、弧、弦的关系,在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等。