知识点二:圆心角与圆周角的关系
同弧所对的圆周角等于圆心角的一半,直径所对的圆周角为直角,90°圆周角所对的弦为直径。
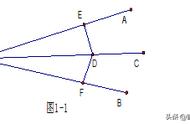
例题2:如图,AB是⊙O的直径,D是弧BC的中点,弦DH⊥AB于点E,交弦BC于点F,AD交BC于点G,连接BD,求证:F是BG的中点.

分析:通过垂径定理、弧与圆心角、圆周角的关系证明∠CBD=∠HDB,通过等角对等边得到FB=FD,再证明∠FDG=∠FGD,得到FD=FG即可解决问题.

因此,圆周角与同弧所对的圆心角相关,那么与之对应的弦、弦心距也可以得到对应关系。

垂径定理及其推论是本章的重点,垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。垂径定理的推论:平分弦(不是直径)的直径垂直与这条弦,并且平分这条弦所对的两段弧。当然,垂径定理的推论不仅仅只有这一个,知识点一种的弦、弧、圆心角三者之间为“知一推二”,而在垂径定理中为“知二推三”。其它推论课本中没有明确给出,我们在解题时可通过全等进行证明。
例题3:⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.