弧长最简单的计算方法,知弦长和拱高求弧长

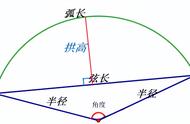
本文主要内容：介绍圆弧的弦长A=5米，拱高H=1米的弦长求法。

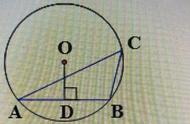
根据题意，有直角三角形关系如下：

R^2=(R-b)^2 (a/2)^2解得：

R=(a^2 4*b^2)/8b，设弧长为L,由公式得：

L=2θR=θ(a^2 4*b^2)/4b.

∵sinθ=(A/2)/R=4ab/(a^2 4*b^2)

∴θ=arcsin[4ab/(a^2 4*b^2)].

即弧长计算表达式为：

L=(a^2 4*b^2)/4b*arcsin[4ab/(a^2 4*b^2)]。

1.泰勒公式定义展开计算

(arcsinx)´=(1-x^2)^(-1/2),则(arcsin0)´=1；

(arcsinx)´´=-(1/2)*(1-x^2)^(-3/2)*(-2x)=x(1-x^2)^(-3/2);

(arcsinx)´´´=(1-x^2)^(-3/2) x[(1-x^2)^(-3/2)]´；

则：(arcsin0)´´=0，(arcsin0)´´´=1.

即arcsinx≈x 0 (1/3!)x^3=x x^3/6=x(x^2 6)/6.此时

arcsin[4ab/(a^2 4*b^2)]

≈4ab[8a^2b^2 3(a^2 4b^2)^2]/[3(a^2 4b^2)^3].

代入弧长计算表达式得：

L≈a[8a^2b^2 3(a^2 4b^2)^2]/[3(a^2 4*b^2)^2]

即：

L≈a [(8/3)a(ab)^2/(a^2 4*b^2)^2].

代入数值计算，得：

L≈5 [(8/3)*5*5^2/(5^2 4*1^2)^2]

L≈5.4。

2.泰勒变形公式展开计算

∵(arcsinx)´=(1-x^2)^(-1/2)

≈1 (-1/2)*(-x^2) (-1/2)*(-3/2)*(-x^2)^2

≈1 (1/2)x^2 (3/4)x^4

∴arcsinx=∫(1-x^2)^(-1/2)dx

≈x (1/6)x^3 (3/20)x^5.对本题有：

arcsin[4ab/(a^2 4*b^2)]≈[4ab/(a^2 4*b^2)]

(1/6)[4ab/(a^2 4*b^2)]^3 (3/20)[4ab/(a^2 4*b^2)]^5.

arcsin[4ab/(a^2 4*b^2)]

≈4ab*{15(a^2 4b^2)^4 40[(ab(a^ 4b^2)]^2

576(ab)^4}/[15(a^2 4b^2)^5]。代入到弧长表达式得：

L≈a*{15(a^2 4b^2)^4 40[(ab(a^ 4b^2)]^2

576(ab)^4}/[15(a^2 4b^2)^4]。即：

L≈a 8a*(ab)^2[5(a^2 4b^2)^2 72(ab)^2]/[15(a^2 4b^2)^4].

代入数值计算，得：L≈

5 40*5^2[5(5^2 4*1^2)^2 72*5^2]/[15*(5^2 4*1^2)^4]，

即:L≈5.57。

​可见两种计算方法，都是弦长增量计算法，都存在一定的误差。