基础链接:
1.一条弧所对的圆周角等于它所对的圆心角的一半;
2.弧长公式:l=nπr/180;
3.经过圆心,垂直于弦的直线平分弦;
4.直角三角形斜边上的中线,等于斜边的一半;
5.如果直角三角形的两条直角边长分别为a,b,斜边长为C,那么a² b²=c².
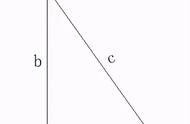
题目:如图1,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求:

图1
(1)弦AB的长;
(2)弦AB所对的劣弧的长.

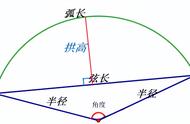
图2
解析:(1)如图2,连接OA,OB,则OA=OB,∠AOB=2∠ACB=90°;
因为点O是圆心,OD⊥AB,
所以AD=BD=1/2AB;
在Rt△AOB中,因为OD是斜边AB边上的中线,
所以OD=1/2AB,
所以AB=2OD=2×2=4.
(2)在Rt△AOB中,因为OA² OB²=AB²,所以2OA²=16,

图3
点拨:勾股定理,圆周角定理,垂径定理,弧长公式是此题求解的依据.
,