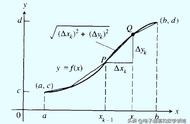
图中黄色部分就是弓形
圆的一条弦把圆分割为两个部分,只要这条弦不是直径,那么这两部分面积不相等,包含圆心的那部分是个弓形,由一段优弧和弦组成;不包含圆心的那部分,是我们最常见的弓形,由一段劣弧和弦组成。一般而言,我们所指的弓形,就是不包含圆心的那个弓形。
相关计算公式见下图:

弓形相关数据计算公式
图上的弓形,如果我们知道弦长s和高度h,就能够求出圆的半径。计算的依据是圆的相交弦定理。
设P是圆内一点,弦AB和弦CD相交于点P,则有AP·PB=CP·PD
请看下图:

弓形已知弦长和高度找圆心计算半径示意图
在弓形CED中,已知弦长CD和高度EF,就可以求出半径R。直径BE垂直平分弦CD,根据相交弦定理,CF·FD=EF·FB,如果我们设圆的半径为R,弦CD的长度为B=2A,弓形高度EF为h,则可以推导出计算半径的公式:
A²=h(2R-h)=2Rh-h² ∴R=(A² h²)/2h
计算实例如下:

计算实例
如图,已知弓形AHB的弦长AB=16,高度CH=4,代入公式计算可得
R=(8² 4²)/2·4=80÷8=10
设:弓形的弦长为b,弓形的高为h, 半径为: R, 弧长为: L, 圆心角为: θ,
计算圆心角的公式为:
θ=4arctan(2h/b).(单位为:弧度).
计算弧长的公式为:
L=2πR*( θ/360)
弧度和角度的转换公式:
弧度记为rad,角度记为deg,1πrad=180°,2πrad=360°
1rad=180°/π(约等于57.29577951°)
公式见下图: